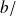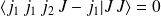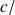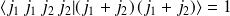Cas de deux Moments
Dans ce cas le moment résultant s'écrit :
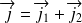(attention cependant, car l'écriture vectorielle est abusive !)
Si le système est soumis à une interaction qui laisse les composantes individuelles inchangées (particules indépendantes) :
et
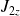sont des constantes du mouvement.
On peut trouver une base commune à
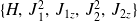formée par les kets :
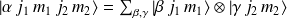
tel que :
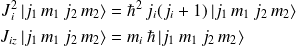
et
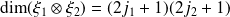. C'est la base découplée.
On peut également choisir une autre base commune à
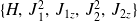tel que :
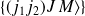où
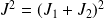et
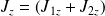
et
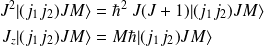. C'est la base couplée.
Coefficients de Clebsch-Gordan
Il existe une transformation unitaire qui permet de passer de la base découplée à la base couplée et vice versa : les vecteurs de l'une s'écrivent comme une combinaison linéaire de vecteurs de la seconde et les coefficients du développement sont appelés coefficients de Clebsch-Gordan (CG) :
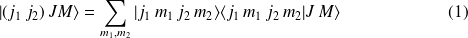
où
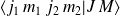sont les coefficients CG.
Règles de sélection sur M
Par souci d'allégement d'écriture, on notera
.
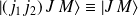Partant de l'équation aux valeurs propres de
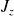on a :
d'où on déduit la première règle de sélection :
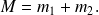
On déduit également la deuxième règle de sélection (ou encore théorème fondamental d'addition) :
.
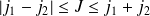Pour une valeur permise de
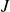, on associe un sous-espace (de Hilbert) de dimension
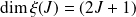tel que :
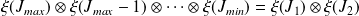
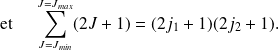
Le moment résultant de l'addition des deux moments associés chacun à une particule s'écrit :
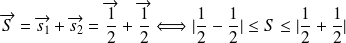
Soit
.
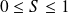On vérifie que :
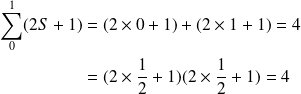
Pour
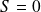, l'état est un singulet :
\\
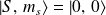Pour
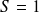, l'état est un triplet :
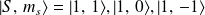
Or, nous avons :
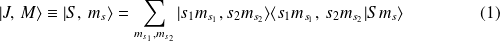
et ainsi nous avons,
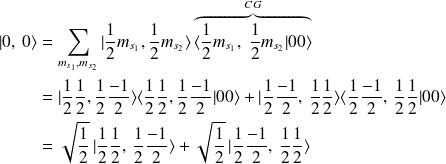
On associe
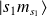à l'état du proton et
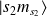à celui du neutron. On a :
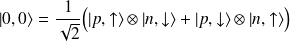
et de la même manière :
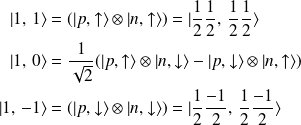
Notations spectroscopiques
Pour un système décrit par un moment orbital
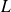et un moment de spin
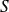, les états quantiques sont désignés par :
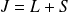étant le moment total et
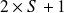la multiplicité.
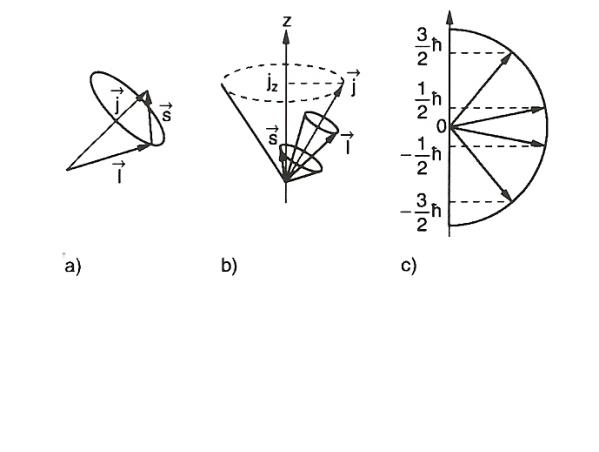
Addition de deux moments. a) Le moment total est obtenu en additionnant les moments orbital
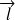et de spin
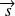, b) précession du moment total autour de l'axe
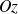, c) valeurs de la composante
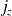pour
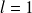et
.
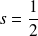Calcul des coefficients de Clebsch-Gordan
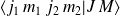existe lorsque :
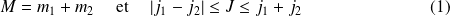
On rappelle l'expression permettant le passage de la base couplée à la base découplée et réciproquement :
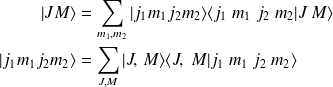
On admet que le coefficient de Clebsch-Gordan
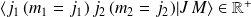et que, pour
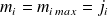, on a
;
.
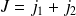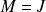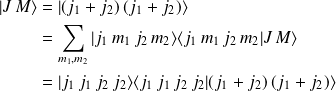
car
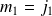et
.
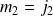Il vient,
.
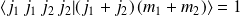A partir de ces relations, on calcule les coefficients C-G par récurrence.
On impose (la justification sera apportée lors des calculs) que :
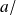les C-G sont tous réels :
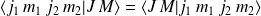
Relation de récurrence
Par application des opérateurs d'échelle à l'expression \ref{JM}, on obtient :
%
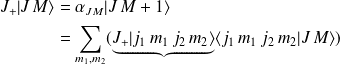
Or,
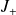agit sur chaque sous-espace
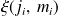par sa restriction
:
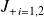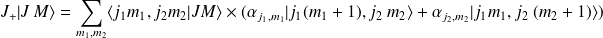
En projetant sur les vecteurs
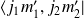, on obtient :
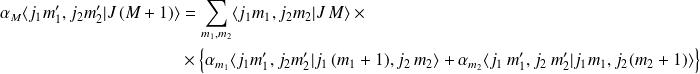
La règle de sélection sur
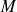implique :
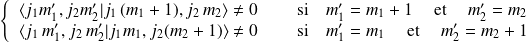
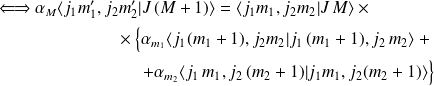
De la même manière, par application de
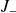(en remplaçant
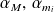par leurs expressions), on obtient :
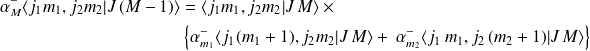
où :
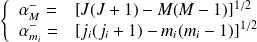
Soit,
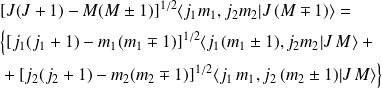
A partir de ces deux relations de récurrence entre les coefficients, et connaissant l'un d'entre eux, il est possible de calculer tous les autres.
Exemple de calcul des C-G
Soit une particule de moment cinétique orbital
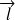et de spin
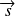. On cherche à calculer les coefficients de Clebsch-Gordan qui permettent le passage de la base couplée
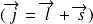à la base découplée
.
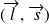La base découplée est notée
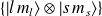et la base couplée
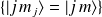. (Pour alléger la notation on écrira
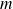lorsqu'il s'agit de
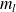). Ainsi, on a :
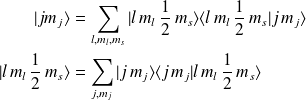
On fait agir sur l'état
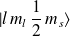l'opérateur
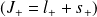tel que :
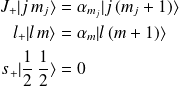
On obtient :
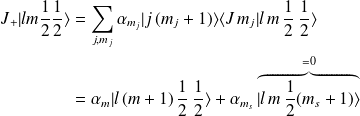
où nous avons utilisé la relation \ref{s+0}. On projette, comme précédemment, sur le bra
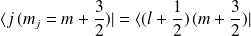. Soit,
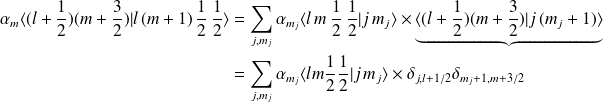
avec,
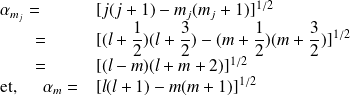
En reportant dans les équations précédentes, on écrit :
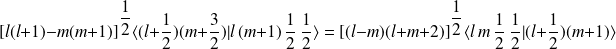
On obtient alors la relation de récurrence :
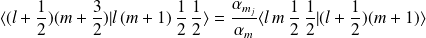
avec :
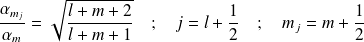
Relations d'orthogonalité
Nous avons déj à vu que coefficients de Clebsch-Gordan sont les coefficients d'une transformation unitaire permettant de passer de la base
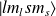à
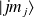et vice versa. Ils vérifient la relation :
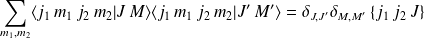
où
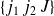désignent les coefficients
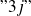tels que :
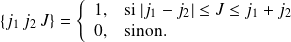
Remarque : Dans le cas d'addition de
moments cinétiques, on définit les C-G généralisés qui sont des sommes de produits de C-G.
Dans le cas d'une particule de moment orbital
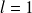et de spin
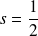, comme indiqué sur la table, si on veut exprimer l'état correspondant à
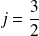et
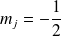en fonction des vecteurs de la base découplée, on a :
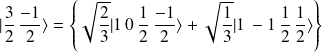
Coefficients de Clebsch-Gordan, harmoniques sphériques et orbitales
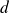. Le symbole de la racine carrée doit être pris en compte pour tous les coefficients :
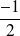signifie
.
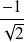