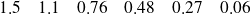Cours de Mécanique Quantique I

Exercice 1 (Rayonnement du Corps Noir)

La loi de Planck pour le rayonnement du corps noir s'écrit en fonction de la

longueur d'onde \lambda sous la forme :

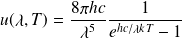
avec 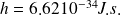, 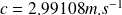et .

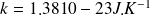1. Montrer que 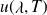et 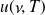sont reliées par la relation :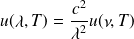

   

2. Montrer que pour les grandes longueurs d'ondes, la loi de Planck se réduit à la loi de Rayleigh-Jeans.

3. On désigne par 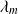la longueur d'onde pour laquelle 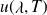est maximale (pour une température 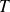fixée), retrouver la loi de Wien : 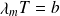où 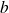est une constante dont on demande de déterminer la valeur.

4. Calculer la densité totale d'énergie et déduire la loi de Stefan.

Exercice 2 (Loi de Wien)

En utilisant la loi de Wien : 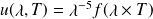, où on rappelle que 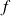est une fonction du produit 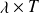, montrer que :

1. si la distribution spectrale du rayonnement d'un corps noir 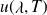est connue à une température 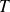donnée alors on peut l'obtenir pour n'importe quelle autre température 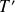(ainsi, l'allure représentative du rayonnement du corps noir est la même quelque soit la température d'où le caractère universel de ),

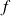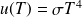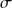2. la puissance totale émise s'écrit où est une constante (il s'agit de la loi de Stefan-Boltzmann),

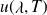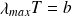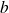3. la longueur d'onde pour laquelle atteint son maximum vérifie la relation : où est une constante (c'est la loi de déplacement de Wien).

Exercice 3 (Effet photoélectrique)

1. La cathode d'une cellule photoélectrique reçoit un rayonnement de longueur d'onde 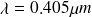et débite un courant 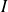que l'on peut annuler en portant l'anode de la cellule à un potentiel de 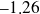Volts plus bas par rapport à la cathode.

1. Calculer le potentiel d'extraction 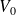de cette cathode.

2. L'énergie d'extraction pour le lithium est .

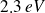• Trouver la longueur d'onde seuil pour l'effet photoélectrique,

• Si une lumière ultraviolette de longueur d'onde 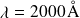tombe sur une surface en lithium, calculer l'énergie cinétique maximale des photoélectrons et la valeur du potentiel d'arrêt.

Exercice 4 (Effet Compton)

On considère un photon incident (particule 1) caractérisé par sa longueur d'onde 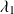, son impulsion 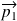et son énergie 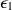. Il rencontre un électron (particule 2) libre au repos de masse 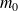, en un point 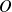. On constate après le choc que l'électron et le photon sont diffusés dans un même plan :

- pour le photon la longueur d'onde devient 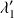, l'impulsion 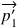et l'énergie 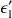, il est diffusé dans la direction .

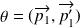- L'électron part avec l'impulsion 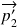dans la direction 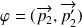, son énergie est 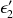et son énergie cinétique est .

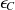1. Trouver la relation donnant 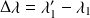en fonction de 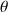et de la longueur d'onde Compton .

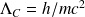2. Déterminer l'énergie 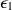du photon incident en fonction de 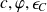et .

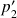Exercice 5 (Ondes de de Broglie)

Calculer les longueurs d'ondes associées aux corpuscules matériels suivants :

• un grain de poussière de 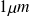de diamètre, de masse 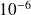kg et de vitesse ,

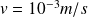• une voiture de masse 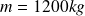roulant à la vitesse de ,

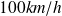• un électron accéléré sous une d.d.p. de ,

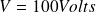• un neutron thermique ( ).

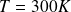  Quelles remarques peut-on faire ?

Exercice 6 (Ondes de de Broglie)

1. Montrer que pour une particule relativiste de quantité de mouvement 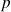et de masse 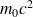on peut écrire : .

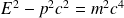2. En déduire l'expression de la quantité de mouvement pour le photon (de masse au repos nulle)

3. On considère une particule de charge 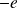et de masse 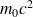accélérée par une d.d.p. :

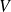• montrer que la longueur d'onde associée à cette particule a comme expression en cinématique relativiste :

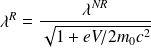  où

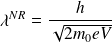
• à partir de quelle valeur de 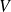devra-t-on utiliser 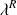pour un électron ? Pour un proton ?

• calculer 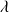pour un électron et pour un proton accélérés sous des d.d.p. de 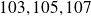et .

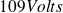Exercice 7 (Expérience de Millikan)

On mesure la contre-tension (ou tension d'arrêt) 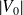d'une cellule photoélectrique à plusieurs longueurs d'ondes, les résultats sont les suivants :

2. tracer la courbe 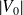en fonction de la fréquence. En déduire la fréquence

seuil .

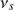3. déterminer :

• la longueur d'onde seuil,

• le travail d'extraction de la surface photosensible,

• la valeur de la constante de Planck à partir de la courbe .
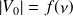