Cours de Mécanique Quantique I

Exercice 1

Soit une particule de masse au repos 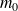, d'énergie 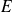et d'impulsion 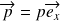. On suppose que cette particule n'est soumise à aucune force extérieure (son mouvement est donc uniforme dans le repère d'étude). On suppose aussi qu'il existe une fonction d'onde associée à cette particule se propageant dans la direction de mouvement et telle que :

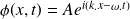
1. Rappeler les expressions des vitesses de groupe 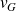et de phase 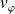. On admet que la vitesse de groupe est égale à la vitesse de la particule. Justifier cette hypothèse.

2. Exprimer l'énergie de la particule en fonction de 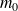et . En utilisant l'hypothèse de de Broglie pour l'énergie de cette particule calculer 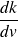. Comparer 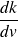et 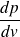. En admettant que 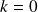pour 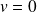, en déduire la relation de de Broglie pour l'impulsion

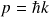
3. Des deux relations de de Broglie, déduire la relation de dispersion lian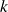t et 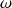. Trouver la relation entre 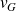et 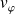. Application : que deviennent ces relations si la particule est un photon ?

4. De l'équation de dispersion, déduire que la fonction 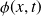décrivant l'onde associée à la particule, satisfait l'équation de Klein-Gordon :

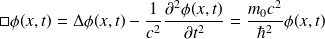
montrer que, dans l'approximation non relativiste, on peut écrire :

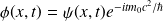
après avoir exprimé 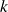et 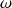en fonction de 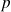. Montrer que pour décrire la probabilité de présence de la particule on peut utiliser s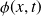oit soit 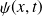. Trouver l'équation différentielle satisfaite par 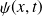. Est-elle plus simple que celle satisfaite par 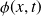? Quelle est cette équation ?

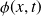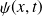5. Comparer pour les deux ondes décrites respectivement par et , les vitesses de phase et les vitesses de groupe. Conclure.

Exercice 2

Considérons une particule libre, dont la fonction d'onde à l'instant 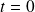s'écrit :

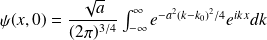
Ce paquet d'ondes est obtenu par superposition d'ondes planes 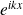avec des coefficients (fonctions de Gauss) :

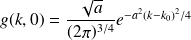
1. Montrer que :

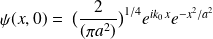
2. Vérifier que la fonction d'onde est de carré sommable.

3. On définit la largeur 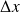d'une fonction de gauss 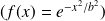par :

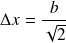
   i. Calculer la largeur 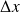de la densité de probabilité

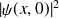
   ii. Calculer la largeur 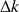de la fonction

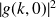
   iii. Vérifier le principe d'incertitude de Heisenberg.

Indications : pour 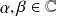, on donne le résultat (à démontrer) :

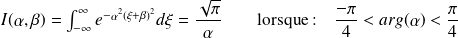
Exercice 3

Une particule est astreinte à se déplacer le long d'un axe 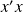. Pour 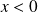, le champ de forces agissant sur la particule est nul (il dérive d'un potentiel constant qu'on prend dans ce cas nul), la particule possède une énergie purement cinétique 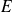constante. Pour 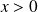, le potentiel est tel que : .

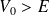1. Décrire le comportement de la particule en mécanique classique lorsqu'elle se dirige de 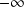vers .

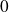2. En mécanique quantique, écrire l'équation de Schrödinger dans les deux régions de l'espace et trouver les fonctions d'onde.

3. Calculer la densité de probabilité en un point 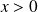. Discuter le résultat.

4. On suppose qu'à la distance 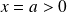, le potentiel s'annule à nouveau. Que peut-on conclure quant à la probabilité de trouver la particule au delà de 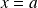? Donner des exemples de phénomènes impliquant un tel résultat.

Exercice 4 (puits de potentiel infini)

On considère une particule plongée dans un puits carré infini de largeur (centré sur ).

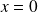1. Montrer que la fonction d'onde normalisée s'écrit :

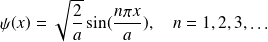
2. Représenter les 4 premières fonctions.

3. Montrer les relations suivantes sur les valeurs moyennes :

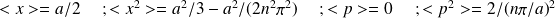
4. En déduire l'expression de 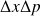. Conclure.

Indication : On donne les intégrales :

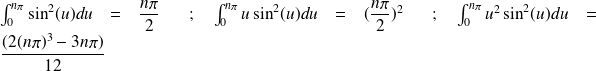
Exercice 5 (Potentiel périodique)

Soit un potentiel périodique de période :

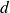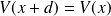
• Montrer que : .

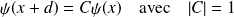• On pose alors : 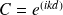et l'on définit la fonction 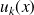par 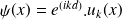. Montrer que 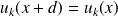. Conclusion.