Exercices
Exercice 1
A partir de l'expression de la densité de probabilité de présence d'une particule :
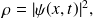démontrer que
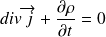en introduisant le vecteur densité de courant de probabilité
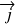tel que :
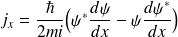
Justifier alors l'expression du coefficient de transmission
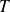sachant que la définition de ce coefficient est :
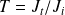où
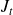et
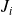représentent respectivement les densités de courant transmise et incidente.
Exercice 2
On considère les opérateurs suivants qui agissent sur des fonctions de la variable
:
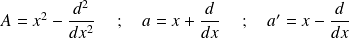
1. Etablir la relation entre opérateurs :
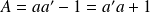. En déduire
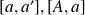et
.
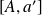2. Soit
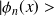une fonction propre de
,
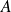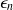la valeur propre correspondante. Montrer que les fonctions
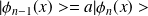et
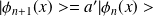sont également fonctions propres de
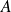. Calculer les valeurs propres correspondantes
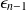et
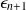en fonction de
.
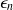Exercice 3
On considère les deux représentations
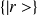et
.
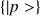Ecrire les relations de fermeture et d'orthonormalisation relatives à ces deux bases et calculer l'expression
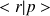.Calculer les éléments de matrice
,
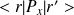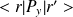et
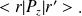
Calculer l'élément de matrice
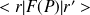où
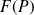est une fonction de l'opérateur
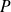.Calculer l'élément de matrice
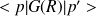où
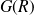est une fonction de l'opérateur
.
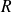Exercice 4
On considère un système quantique dont le vecteur d'état à l'instant
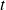est donné par :
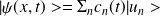où les
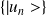forment une base orthonormée, complète et discrète de l'espace des états et les
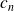sont tels que
.
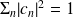Soit l'opérateur défini par :
.
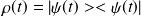Montrer que
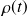est hermitien et que
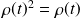. Calculer ses éléments de matrice
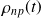dans la base
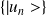et montrer que
.
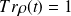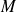étant une observable attachée au système montrer que sa valeur moyenne est :
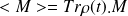
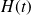étant le hamiltonien du système, montrer que l'opérateur
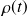vérifie l'équation d'évolution :
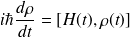
On suppose que
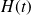peut se mettre sous la forme :
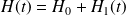. On pose et donner l'équation de
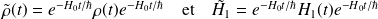. Donner l'équation de
