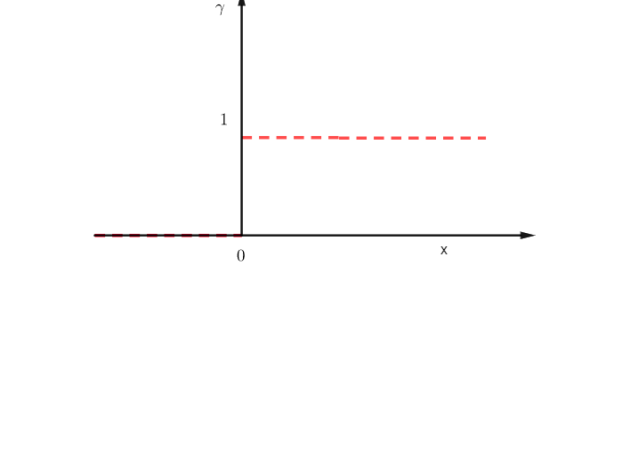
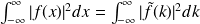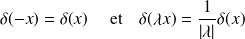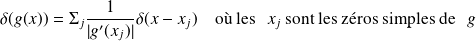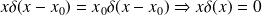Rappels Mathématiques
Distribution de Dirac
Ce sont des fonctions densités qui décrivent une répartition d'une certaine quantité dans un matériau (dans "l'espace" considéré):
Exemples : distribution de charge linéique
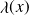, de surface
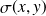, dans un volume
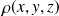tel que
respectivement,
,
,
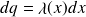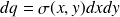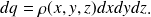
Distribution de Dirac : C'est la distribution élémentaire constituée d'une unité de la grandeur considérée concentrée en un point origine.
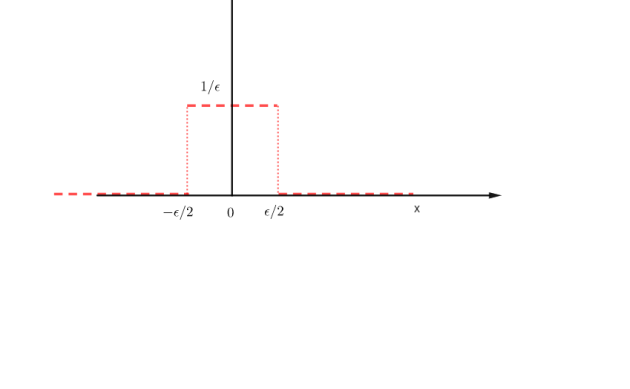
Exemple : Soit la fonction
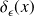définie par
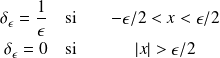
et si
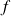est une fonction quelconque continue à l'origine, on a
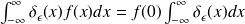
Si on pose :
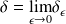, alors on définit
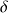par
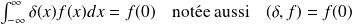
Si l'origine est
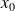, alors :
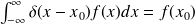
Remarque :
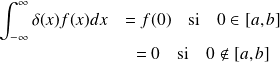
Propriétés
Primitive de
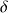: soit
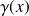tel que :
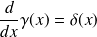
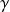est appelée fonction de Heaviside est définie comme suit :
Dérivée de
:
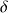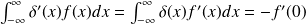
Propriétés
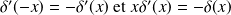
généralisation :
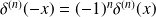et
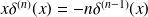
Transformée de Fourier
La tranformée de Fourier
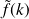de
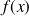est par définition :
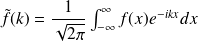
et réciproquement,
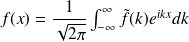
Egalité de Bessel-Parseval : La transformée de Fourier conserve la norme
