Systèmes de Particules Identiques
Définition :
Soit un système de
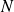particules identiques préparées dans le même état quantique
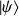. Les
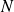particules sont supposées indépendantes entre elles. Soit
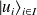la base dans laquelle on exprime
:
.
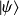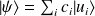Elle est identique pour toutes les particules. On notera les particules de coordonnées
.
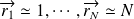L'état décrivant les
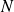particules noté
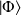s'écrit comme un produit tensoriel des
:
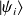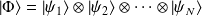
L'espace total
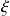est l'espace produit tensoriel des espaces
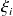associés à chacune des
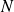particules :
tel que
Remarque :
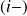Cas d'une seule particule :
En fait,
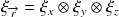et
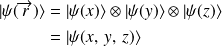
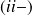Si la particule admet un degré de liberté (
, par exemple)
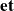un autre de structure intrinsèque (spin), l'état qui la décrit est :
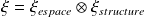et :
Le produit tensoriel est linéaire et distributif.
Si
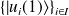est une base de
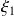et
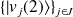une base de
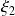, alors
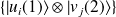est une base de
.
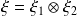Ainsi, soit
et
. Un état résultant du produit tensoriel de ces deux états s'écrira :
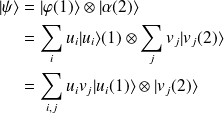
L'état
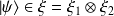est dit
.
Tous les états de
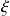(espace des états) peuvent être décomposés en combinaison linéaire de produits tensoriels. Il existe cependant des états de
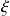qui s'écrivent sous la forme :
et où
.
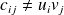Par conséquent, un tel état ne peut pas s'écrire sous la forme
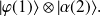
Etant donné deux vecteurs d'états :
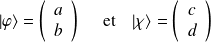
alors, en représentation matricielle, l'état produit tensoriel des deux s'exprime comme suit :
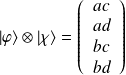
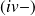Expression des opérateurs :
Soit
un opérateur agissant sur les états de
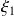et
sur ceux de
.
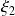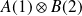désigne leur produit tensoriel. Soit
.
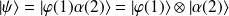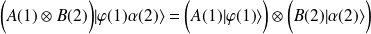
Si l'action de l'opérateur
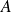se limite aux vecteurs propres (états propres) de
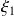seulement, son prolongement dans l'espace
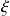s'écrit :
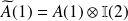
tel que :
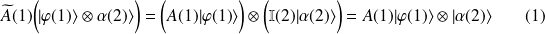
La représentation matricielle du produit tensoriel (relativement à une base donnée) est de la forme :
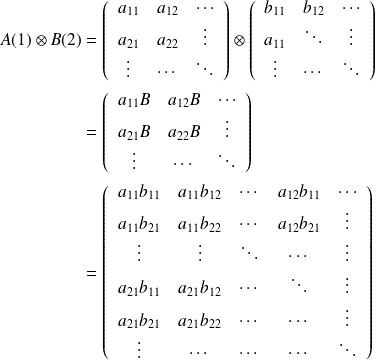
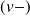L'étude de l'interaction d'un champ électromagnétique avec un système physique (atome, molécule, solide etc.) s'effectue dans beaucoup de situations de manière semi-classique, le système physique est quantifié mais la radiation est introduite de façon phénoménologique, i.e. on ne s'intéresse pas à sa structure quantique. Un traitement rigoureux consiste à considérer le système
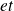la radiation comme un seul système et, alors, un état décrivant ce dernier est obtenu en formant le produit tensoriel des états respectifs de l'atome (ou molécule..) et de la radiation.
La quantification du champ est obtenue grâce au formalisme de seconde quantification et l'état décrivant un mode de vibration noté
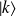, où
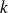représente est un indice qui tient compte de la polarisation des ondes
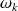composant le champ. L'état de l'ensemble ainsi obtenu peut s'écrire sous la forme :
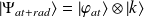
Système de deux particules
Soit
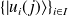la base dans laquelle s'expriment les états associés à deux particules (désignées par
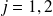), on note ces états :
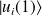et
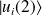avec
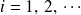. Dans l'espace produit (tensoriel), le vecteur état s'écrit :
Remarque : Les particules n'interagissent pas.
Le hamiltonien du système formé de ces deux particules est
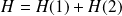. La valeur propre associée est
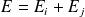. Si
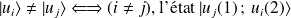est aussi ket propre. Il y a dégénérescence par échange des particules.
Remarques :
Toute combinaison linéaire
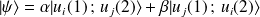est aussi un ket propre, avec
Les particules
et
étant identiques, tout échange devrait donner le même résultat après une mesure. (On peut traduire le comportement de l'état suite à un échange des deux particules en écrivant :
,le "+" correspond aux bosons et le "-" aux fermions). Il y a deux possibilités :
le vecteur d'état est symétrique lorsqu'un échange (permutation) est effectué :
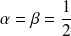, les particules sont des bosons.
le vecteur d'état est antisymétrique si on échange les deux particules :
, les particules sont des fermions.
Définition : Postulat de symétrisation
Le vecteur d'état qui décrit un ensemble de systèmes (particules) identiques doit être soit complètement symétrique (cas des bosons), soit complètement antisymétrique (cas des fermions), par rapport à la permutation (l'échange) de deux systèmes entre eux.
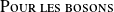
L'état symétrique
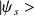s'écrit :
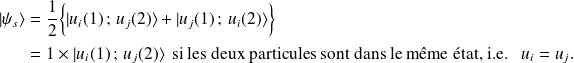
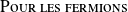
L'état antisymétrique
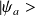s'écrit :
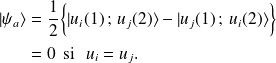
C'est la traduction du principe d'exclusion de Pauli pour deux fermions : ils ne peuvent occuper un même état.
Pou tenir compte de l'antisymétrie de l'état, on écrit
sous la forme d'un déterminant (de Slater) dont les éléments de matrice sont les kets
, tel que :
