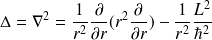Rappels
Dans les sections précèdentes, on a développé, à partir de la définition du moment cinétique
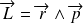, une théorie générale pour un moment cinétique
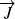. Les valeurs possibles pour
sont soit entières soit demi-entières. Le cas particulier
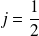(associé au spin de l'électron) a été traité. On considère dans la suite un moment avec des valeurs
entières (en omettant d'abord le spin).
En représentation
:
.
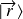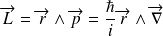En coordonnées sphériques :
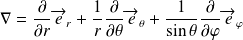
avec,
et
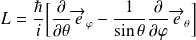
où,
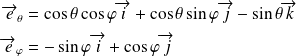
Les composantes
,
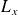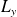et
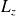de
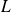s'écrivent :
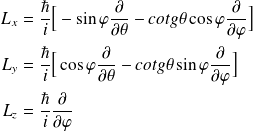
On en déduit les expressions des opérateurs d'échelle :
D'autre part, on peut récrire
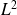sous la forme suivante :
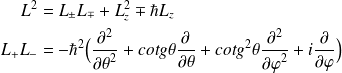
Ce qui donne, en remplaçant dans l'expression de
:
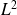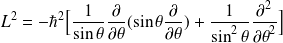
et, en fin, on obtient l'expression du laplacien en coordonnées sphériques :
