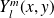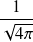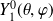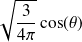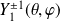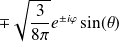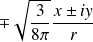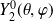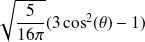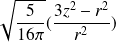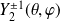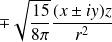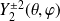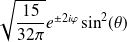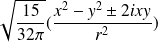Equations aux Valeurs Propres
Fonctions Propres
Les fonctions propres de
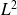 et
et
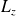 associées aux valeurs propres
associées aux valeurs propres
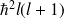 et
et
 respectivement sont solutions des équations :
respectivement sont solutions des équations :
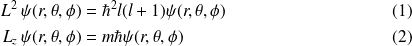
Or,
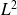 et
et
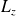 n'ont aucune dépendance de
n'ont aucune dépendance de
 , par conséquent,
, par conséquent,
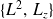 ne forme pas un E.C.O.C.
ne forme pas un E.C.O.C.
L'introduction d'une troisième observable (
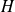 par exemple) permet de compléter l'étude de
par exemple) permet de compléter l'étude de
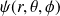 . Ainsi,
. Ainsi,
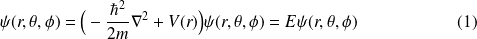
Pour un système dont le hamiltonien
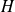 reste invariant sous une rotation
reste invariant sous une rotation
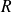 , on a
, on a
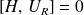 , les fonctions
, les fonctions
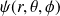 s'écrivent sous la forme :
s'écrivent sous la forme :
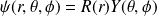
En effet,
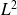 et
et
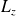 dépendant uniquement de
dépendant uniquement de
 et
et
 , leurs vecteurs communs notés
, leurs vecteurs communs notés
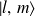 vérifient (en coordonnées sphériques) :
vérifient (en coordonnées sphériques) :
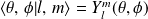
Il vient, en substituant
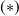 dans
dans
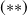 :
:
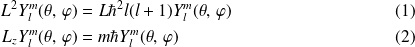
Et, en utilisant la condition de normalisation pour
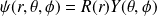 :
:
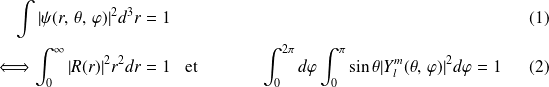
Remarque :
La composante
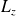 ne dépend que de
ne dépend que de
 , on écrit les harmoniques sphériques
, on écrit les harmoniques sphériques
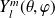 sous la forme séparée :
sous la forme séparée :


Expression des vecteurs et valeurs propes de
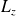
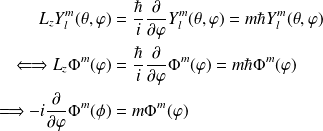
Les solutions normalisées sont :
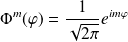
qui satisfait la relation d'orthogonalité :
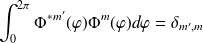
de plus, on doit avoir, en vertu de la périodicité sur
 ,
,
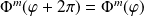 , soit,
, soit,
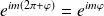
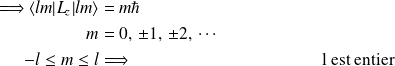
Etats propres de
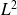
Afin de compléter la dépendance en
 , on procède comme pour
, on procède comme pour
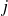 , i.e., pour une valeur donnée de
, i.e., pour une valeur donnée de
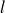 on doit avoir :
on doit avoir :
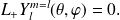
En utilisant l'expression en coordonnées sphériques de
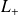 , on a :
, on a :
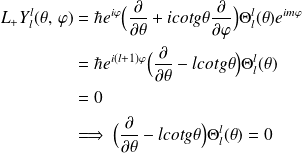
La solution est :
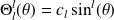
d'où on déduit une expression de l'harmonique sphérique
 :
:
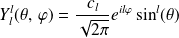
avec
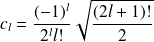
L'action de
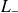 sur
sur
 donne :
donne :

L'action répétée (
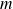 fois) de
fois) de
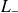 s'exprime comme suit :
s'exprime comme suit :
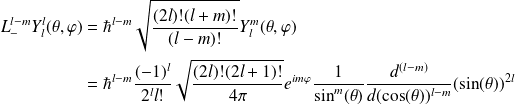
après égalisation, on obtient l'expression de
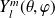 , pour
, pour
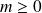 :
:

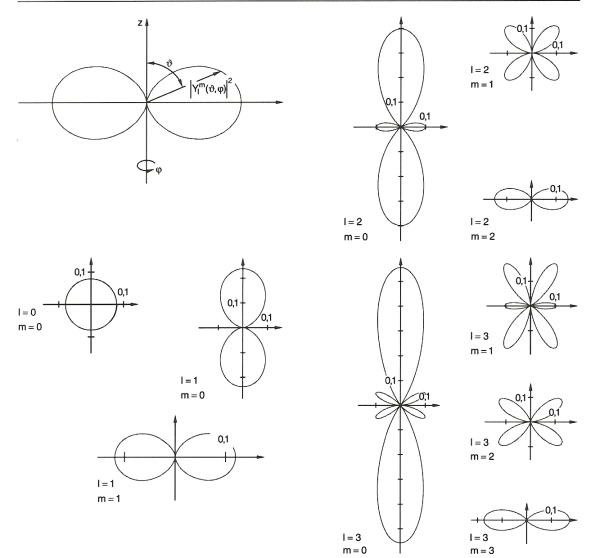
Propriétés des harmoniques sphériques
Les
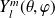 sont des fonctions propres communes à
sont des fonctions propres communes à
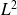 et
et
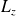 . Elles sont orthonormales (en fait, elles constituent une base orthonormée de l'espace de Hilbert des fonctions de carré sommable en
. Elles sont orthonormales (en fait, elles constituent une base orthonormée de l'espace de Hilbert des fonctions de carré sommable en
 et
et
 ).\ref{Figure-HS}
).\ref{Figure-HS}
la relation de fermeture s'écrit :
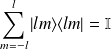
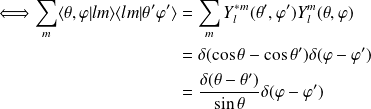
Les
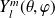 sont complexes :
sont complexes :
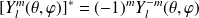
et l'action de l'opérateur parité se traduit par :
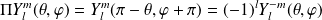
On voit que
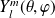 est un état propre de l'opérateur parité
est un état propre de l'opérateur parité
 associé à la valeur propre
associé à la valeur propre
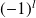 .
.
On peut également établir un lien entre les harmoniques sphériques et les polynômes de Legendre. En effet, ces polynômes sont définis par (où
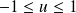 ):
):
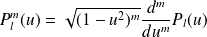
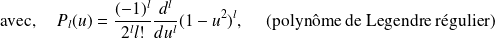
Ainsi,
Cas
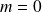
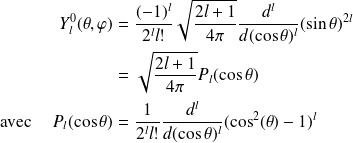
On peut, ainsi, vérifie aisément que
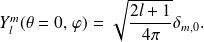
Cas général
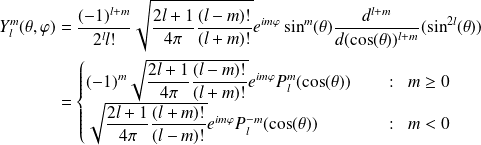
 :
:
 .
.
On peut écrire
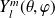 en coordonnées cartésiennes en substituant par les relations
en coordonnées cartésiennes en substituant par les relations
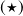 .
.
Exemple :
 et
et
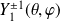
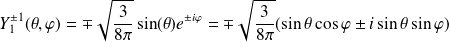

|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En représentation
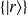 , les fonctions propres associées de
, les fonctions propres associées de
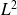 et
et
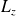 sont les
sont les
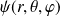 vérifiant les équations \ref{L2} et
vérifiant les équations \ref{L2} et
 . La dépendance radiale (en
. La dépendance radiale (en
 ) n'est pas prise en compte, (
) n'est pas prise en compte, (
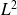 et
et
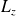 ne forment pas un E.C.O.C.). On doit alors chercher une troisième équation, comme déjà mentionné précédemment, et on doit pouvoir séparer les variables
ne forment pas un E.C.O.C.). On doit alors chercher une troisième équation, comme déjà mentionné précédemment, et on doit pouvoir séparer les variables
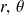 et
et
 . Ceci est réalisé si on écrit :
. Ceci est réalisé si on écrit :
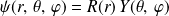
L'équation aux valeurs propres pour un hamiltonien (supposé de symétrie centrale, comme c'est le cas des hydrogénoïdes qui sera traité plus loin) permet d'obtenir cette troisième équation.