Définitions
On a vu dans ce qui précède comment établir le caractère corpusculaire de la lumière, comment associer un caractère ondulatoire à un corpuscule et, enfin, comment, partant de cette dualité (aussi bien pour le corpuscule que pour la lumière), introduire la notion de fonction d'onde (ou onde de probabilité) permettant d'interpréter les franges d'interférences obtenues avec des corpuscules. Il reste à établir l'équation à laquelle doit satisfaire cette fonction d'onde. C'est l'objet de la mécanique ondulatoire développée par L. de Broglie et Schrödinger.
Fonction d'Onde
(i) L'état quantique d'un corpuscule est caractérisé par une fonction d'onde
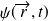 .
.
(ii)
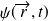 est interprétée comme l'amplitude de probabilité de position. La probabilité de trouver la particule, au cours d'une mesure, à l'instant t, dans l'élément de volume
est interprétée comme l'amplitude de probabilité de position. La probabilité de trouver la particule, au cours d'une mesure, à l'instant t, dans l'élément de volume
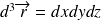 autour du point
autour du point
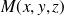 est:
est:
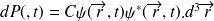 ,
,
où
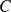 est une constante de normalisation tel que :
est une constante de normalisation tel que :
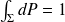 et
et
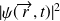 définit la densité de probabilité (donc
définit la densité de probabilité (donc
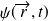 doit être de carré sommable).
doit être de carré sommable).
(iii) Principe de décomposition spectrale: Si l'on veut mesurer une grandeur
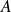 , le résultat appartient à un ensemble
, le résultat appartient à un ensemble
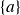 de valeurs propres telles que :
de valeurs propres telles que :•
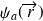 est une fonction propre à laquelle est associée le valeur propre
est une fonction propre à laquelle est associée le valeur propre
 :
:
•
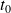 étant l'instant de la mesure :
étant l'instant de la mesure :
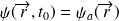
La probabilité
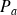 de trouver, lors de la mesure, à l'instant
de trouver, lors de la mesure, à l'instant
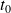 , la valeur propre
, la valeur propre
 s'obtient en décomposant
s'obtient en décomposant
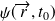 sur les fonctions propres
sur les fonctions propres
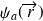 :
:
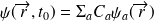
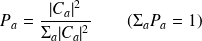
Application: cas de l'hydrogène
Soit la position
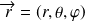 .
.
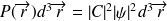
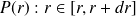
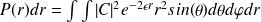
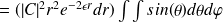
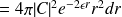
Lorsque
 tend vers
tend vers
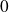 ,
,
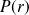 tend vers
tend vers
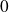 et lorsque
et lorsque
 tend vers
tend vers
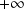 ,
,
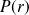 tend vers
tend vers
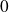 .
.
Le maximum de probabilité de présence (en posant
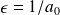 ):
):
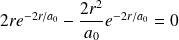
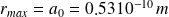 rayon de Bohr.
rayon de Bohr.
Soit une particule libre se mouvant le long de l'axe
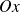 (cas unidimensionnel). On a vu que l'on peut écrire (d'après la dualité onde-corpuscule):
(cas unidimensionnel). On a vu que l'on peut écrire (d'après la dualité onde-corpuscule):
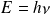 et
et
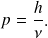
En introduisant la pulsation
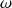 et le vecteur d'onde
et le vecteur d'onde
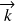 :
:
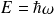 et
et
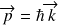
Cela revient à associer à cette particule (
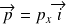 ) une onde de vecteur d'onde
) une onde de vecteur d'onde
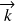 , tel que :
, tel que :
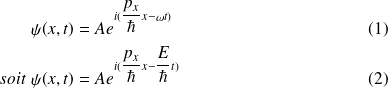
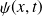 satisfait aux relations :
satisfait aux relations :
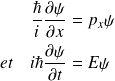
Remarque :
(i) Même dans le cas où la particule n'est pas libre, la mécanique ondulatoire postule que les variables dynamiques
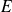 et
et
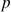 sont toujours écrites sous cette forme.
sont toujours écrites sous cette forme.(ii) Il ne s'agit pas ici d'une vibration comme dans l'électromagnétisme (EM), mais de l'amplitude de probabilité associée à la particule.
(iii)
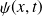 est décrite par une onde plane (OP) qui n'est pas de carré sommable et, par conséquent, ne peut représenter un état physique.
est décrite par une onde plane (OP) qui n'est pas de carré sommable et, par conséquent, ne peut représenter un état physique.
Paquet d'Ondes
Une superposition d'ondes planes peut être de carré sommable, on associera donc à une particule une superposition de ces ondes appelée paquet d'ondes.
Si l'onde plane satisfait à une équation de propagation ( comme les vibrations en EM) alors le paquet d'onde (qui est une somme de fonctions de ce type) y satisfait également :
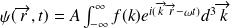
où
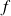 est une fonction régulière,
est une fonction régulière,
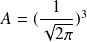 et
et
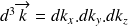 .
.
Cas unidimensionnel :
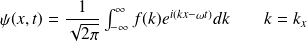
à
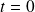 ,
,
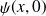 est la transformée de Fourier de
est la transformée de Fourier de
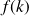 :
:
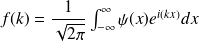
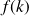 détermine la forme du paquet d'ondes, elle module les ondes planes qui composent celui-ci. La forme dépend donc de
détermine la forme du paquet d'ondes, elle module les ondes planes qui composent celui-ci. La forme dépend donc de
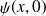 .
.
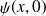 est maximale lorsque les ondes planes interférent de manière constructive et s'annule loin de ce maximum.
est maximale lorsque les ondes planes interférent de manière constructive et s'annule loin de ce maximum.
On cherche le maximum de
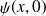 auquel correspond le centre du paquet d'onde. Soit
auquel correspond le centre du paquet d'onde. Soit
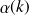 l'argument de
l'argument de
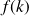 tel que :
tel que :
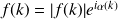
et
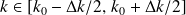 intervalle centré autour de
intervalle centré autour de
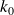
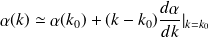
il vient :
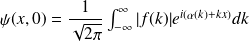
On reporte l'expression de
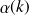 et
et
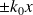 :
:
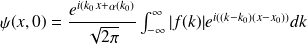
où on a posé
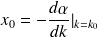 (
(
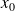 est la position du centre du paquet d'onde).
est la position du centre du paquet d'onde).
D'une manière générale:
Si on prend
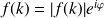 où
où
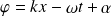
les plus grandes valeurs de
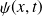 seront obtenues pour
seront obtenues pour
 :
:
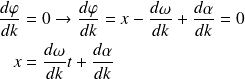
On définit alors la vitesse de groupe du centre du paquet d'onde :
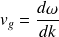
Remarque :
i)
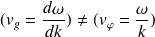
ii) pour un paquet d'ondes lié à la particule il faut que
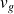 soit égale à la vitesse de la particule :
soit égale à la vitesse de la particule :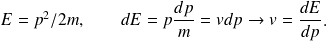
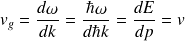 .
.
Application :
Paquet d'ondes à
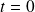 . Cas
. Cas
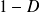 :
:
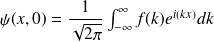
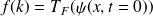
Superposition de 3 ondes :
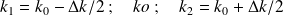
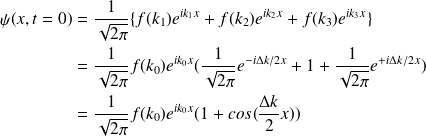
•
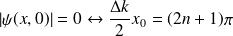 .
.
•
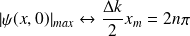 .
.
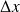 est l'intervalle entre deux zéros consécutifs :
est l'intervalle entre deux zéros consécutifs :
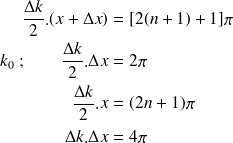
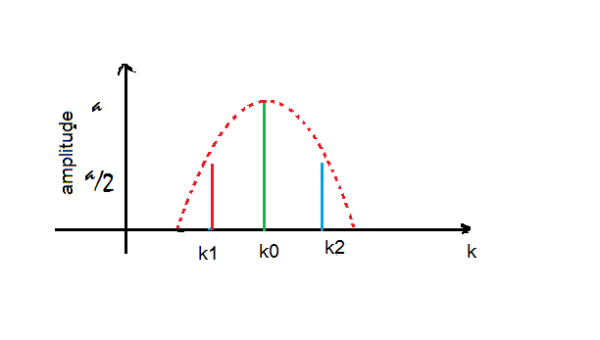
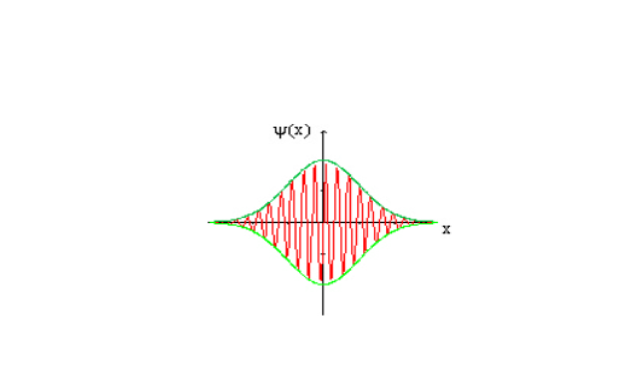
Représentation d'un paquet d'ondes
Au centre (
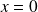 ) les ondes interfèrent de façon constructive plus loin, en raison de leur déphasages, leur somme s'annule. A partir d'ondes illimitées (
) les ondes interfèrent de façon constructive plus loin, en raison de leur déphasages, leur somme s'annule. A partir d'ondes illimitées (
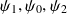 ) on obtient par leur superposition une onde limitée dans l'espace (son étendue
) on obtient par leur superposition une onde limitée dans l'espace (son étendue
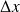 est telle que :
est telle que :
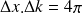 ).
).
Remarque :
Ce paquet d'onde représente l'état d'une particule dont la probabilité de présence (à
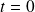 ) est nulle en dehors d'un intervalle de largeur
) est nulle en dehors d'un intervalle de largeur
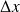 :
:
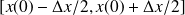 .
.
Conséquence fondamentale :
En écrivant :
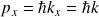 et
et
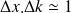
il vient :
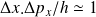
Soit

Ces relations qui traduisent le principe d'incertitude de Heisenberg sur la position et la quantité de mouvement ont une portée fondamentale sur la notion de "mesure".
• Si au cours d'une mesure sur un ensemble de particules identiques on détermine la position d'une particule dans une région "étalée" de
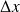 , alors la mesure (simultanée) de l'impulsion d'une particule de ce système donne des résultats dans un intervalle de largeur
, alors la mesure (simultanée) de l'impulsion d'une particule de ce système donne des résultats dans un intervalle de largeur
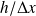 .
.
Inversement, la mesure de l'impulsion avec une grande précision, donne un résultat de la position dans l'intervalle
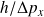 .
.
Equation de Schrödinger
On vient de voir comment associer une onde à une particule à travers un paquet d'ondes planes. On a vu aussi que cette onde (ou paquet d'ondes) doit satisfaire à une équation de "propagation" comme c'est le cas des vibrations en EM.
La fonction d'onde
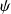 d'un système microscopique (quantique) définit entièrement son état dynamique (
d'un système microscopique (quantique) définit entièrement son état dynamique (
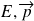 ). Par conséquent, on doit imposer à l'équation de propagation certaines condition :
). Par conséquent, on doit imposer à l'équation de propagation certaines condition :
* elle doit être linéaire, homogène : si
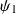 et
et
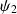 sont deux solutions alors toute combinaison linéaire de
sont deux solutions alors toute combinaison linéaire de
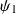 et
et
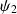 est aussi solution : (
est aussi solution : (
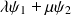 ) pour
) pour
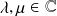 .
.
* elle doit être au premier ordre par rapport au temps : toute évolution ultérieure et déterminée par la donnée de
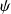 à l'instant
à l'instant
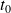 .
.
* à la limite, elle doit conduire à une équation de la mécanique classique.
Cas simple d'une particule libre
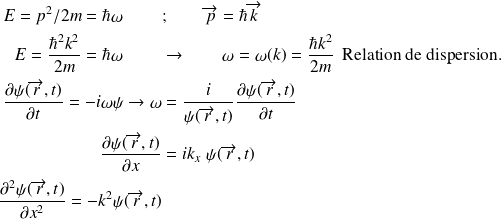
En remplaçant dans l'expression de
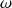 :
:
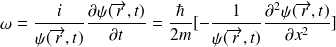
Soit encore :
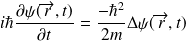
C'est l'équation de Schrödinger pour une particule libre.
Cas d'une particule dans un potentiel
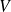 indépendant du temps :
indépendant du temps :
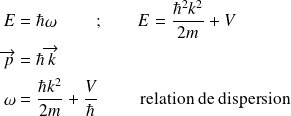
On obtient, après un calcul similaire :
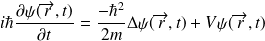
Equation de Schrödinger pour une particule dans un potentiel indépendant du temps : ( particule libre soumise à un champ scalaire).
L'équation de Schrödinger s'écrit :
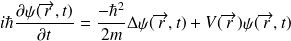
On pose
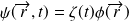 et en remplaçant :
et en remplaçant :
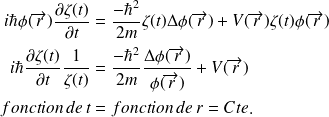
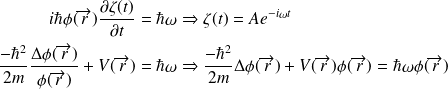
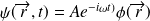 est solution de l'équation de Schrödinger.
est solution de l'équation de Schrödinger.
La densité de probabilité
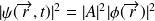 est indépendante du temps.
est indépendante du temps.
(2)
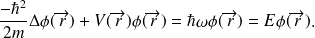
(3) soit, en introduisant le hamiltonien
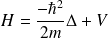 :
:
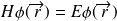
C'est l'équation aux valeurs propres, avec :
•
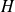 un opérateur linéaire différentiel :
un opérateur linéaire différentiel :
Si
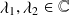 et si
et si
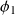 et
et
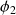 sont deux solutions de
sont deux solutions de
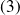 , alors :
, alors :
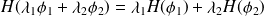
• Les énergies possibles sont les valeurs propres de H
•
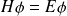 permet de chercher parmi tous les états possibles de la particule ceux qui sont stationnaires.
permet de chercher parmi tous les états possibles de la particule ceux qui sont stationnaires.
Soit
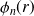 une fonction propre associée à la valeur propre
une fonction propre associée à la valeur propre
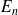 :
:
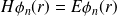
En général :
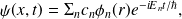
où on a considéré :
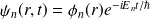 et
et
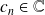 .
.
si
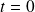 :
:
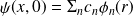 état qui caractérise la particule à
état qui caractérise la particule à
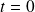 .
.