Applications
Introduction
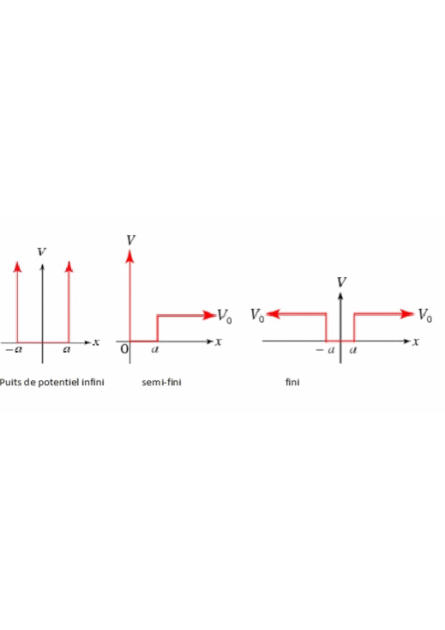
Comportement de la fonction d'onde et représentation d'un potentiel:
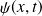 doit représenter l'amplitude de probabilité de présence de la particule dans l'espace. Le potentiel qu'elle rencontre peut être de nature différente (coulombien, nucléaire...) qui varie en fonction de
doit représenter l'amplitude de probabilité de présence de la particule dans l'espace. Le potentiel qu'elle rencontre peut être de nature différente (coulombien, nucléaire...) qui varie en fonction de
 de manière "continue".
de manière "continue".
Cependant, pour représenter ces potentiels, on assimile les zones où ils varient rapidement à des discontinuités.
* En mécanique classique, si
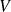 est l'énergie potentielle et
est l'énergie potentielle et
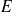 l'énergie totale de la particule, alors les domaines où
l'énergie totale de la particule, alors les domaines où
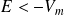 sont interdits. Cela reste vrai en mécanique quantique.
sont interdits. Cela reste vrai en mécanique quantique.
Marche de Potentiel
Marche de potentiel
i) Cas
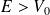 : (réflexions partielles).
: (réflexions partielles).
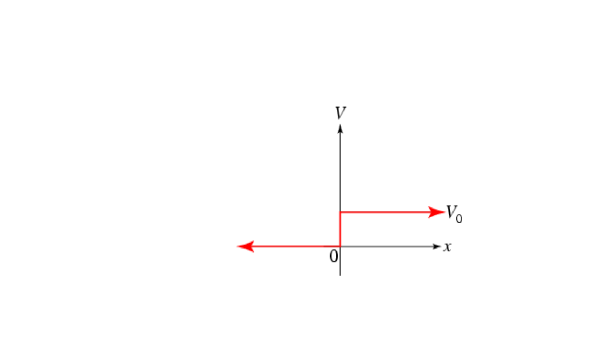
On résout l'équation de Schrödinger pour les deux régions :
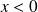 et
et
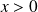
•
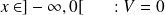
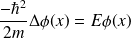
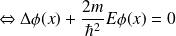 on pose
on pose
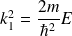
La solution s'écrit :
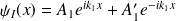 .
.
•

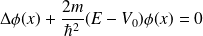 on pose :
on pose :
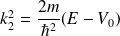
La solution s'écrit :
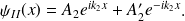
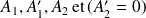 déterminent parfaitement les états stationnaires
déterminent parfaitement les états stationnaires
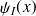 et
et
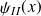 .
.
On cherche à exprimer les quantités
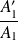 et
et
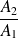 . Pour ce faire, on considère les conditions de raccordement (continuité de
. Pour ce faire, on considère les conditions de raccordement (continuité de
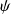 et de sa dérivée
et de sa dérivée
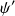 en
en
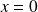 )
)
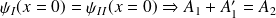
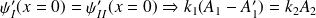
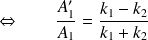 et
et
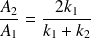
On définit les coefficients de réflexion R :
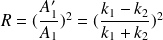
et de transmission T :
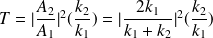
On vérifie aisément que
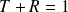
(En optique :
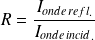 et
et
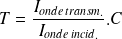
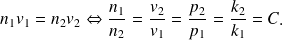 )
)
2. ii) Cas
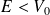
•
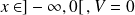 et
et
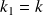
La solution est
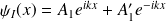
•
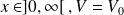
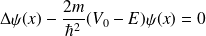 et si on pose :
et si on pose :
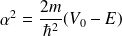
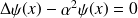
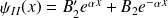
Il s'agit d'une onde évanescente (de portée
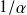 ), la solution physique impose
), la solution physique impose
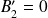 .
.
Conditions de raccordement en
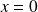
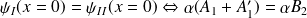
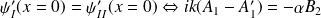
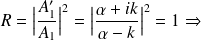 réflexion totale.
réflexion totale.
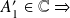 L'onde réfléchie sera déphasée par rapport à l'onde incidente.
L'onde réfléchie sera déphasée par rapport à l'onde incidente.
Barrière de Potentiel
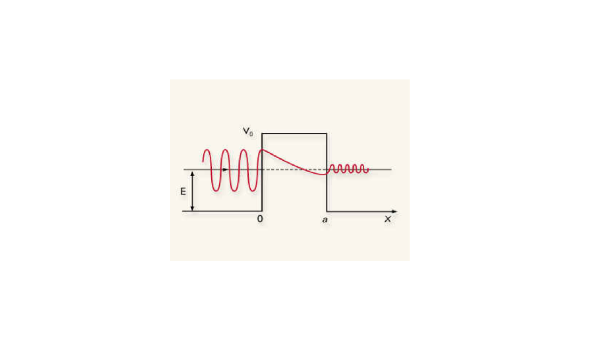
Exemple: un électron arrivant sur le cortège électronique d'un atome.
a)- Cas
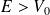 : les solutions de l'équation de Schrödinger sont des ondes planes dans les 3 régions :
: les solutions de l'équation de Schrödinger sont des ondes planes dans les 3 régions :
•
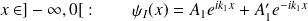 .
.
•
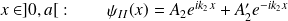 .
.
•
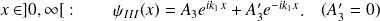
où
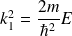 et
et
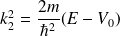
Conditions de raccordement aux points de discontinuité de
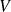 :
:
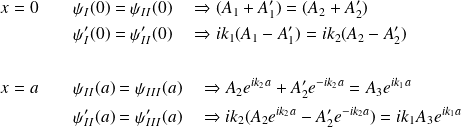
On déduit :
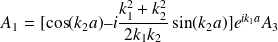
Et
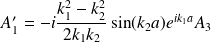
et on définit les coefficients de transmission et de réflexion :
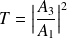 et
et
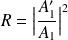
vérifiant
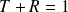 .
.
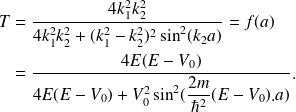
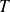 est périodique :
est périodique :
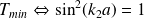 , soit :
, soit :
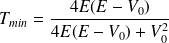 .
.
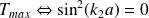 , soit
, soit
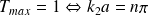 : il y a transmission totale.
: il y a transmission totale.
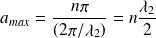 , on a une résonance, onde stationnaire.
, on a une résonance, onde stationnaire.
b)- Cas
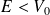 : Les solutions de l'équation de Schrödinger changent :
: Les solutions de l'équation de Schrödinger changent :
• région I :
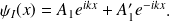
• région II :
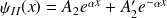 .
.
• région III :
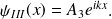
où
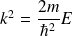 et
et
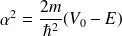
Remarque :
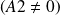
Les conditions aux limites
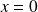 et
et
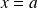 donnent :
donnent :
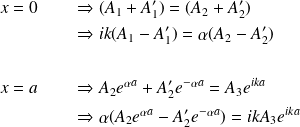
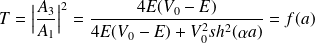
* Si
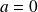 alors
alors
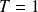
* Si
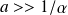 (portée de l'onde) on a
(portée de l'onde) on a
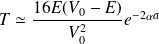
• Si
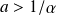 , la probabilité de transmission est négligeable.
, la probabilité de transmission est négligeable.
• Si
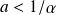 la particule a une probabilité importante de franchir a barrière de potentiel. C'est l'effet Tunnel.
la particule a une probabilité importante de franchir a barrière de potentiel. C'est l'effet Tunnel.
Puits Infini
Une particule confinée dans une boîte dont les parois sont solides ou un électron lié à une molécule linéaire peuvent être représentés par un puits infini. Un exemple tiré de la technologie des semi-conducteurs est une couche de matériau très mince insérée entre deux matériaux isolants ou semi-conducteurs de plus grande bande interdite (
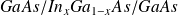 ) où
) où
 désigne la composition. La réduction d'une dimension de la couche entraîne une quantification de l'énergie.
désigne la composition. La réduction d'une dimension de la couche entraîne une quantification de l'énergie.
Soit une particule confinée dans la région
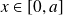 (voir la figure).
(voir la figure).
Le potentiel est représenté par:
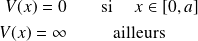
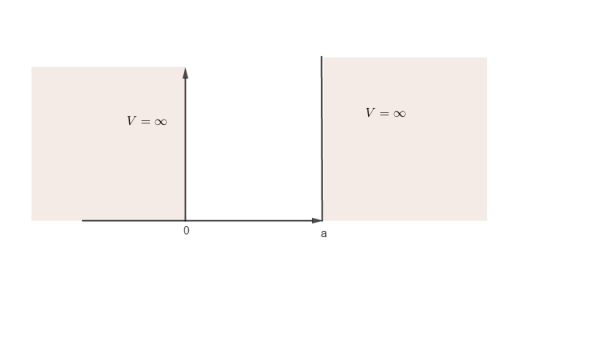
La fonction d'onde doit satisfaire aux conditions de bord (continuité de la fonction d'onde):

L'équation de Schrödinger:
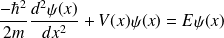
devient
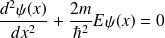
soit, en posant
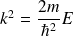 ,
,
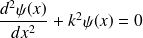
La solution est de la forme:
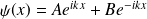
En vertu des conditions de bord, il vient:
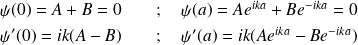
D'où on déduit:
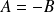 et
et
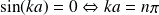 avec
avec
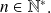
Soit :
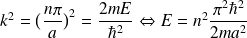
La fonction d'onde s'écrit alors :
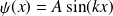 .
.
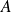 est la constante de normalisation :
est la constante de normalisation :
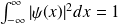
Ce qui donne après calcul :
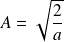 .
.
Soit,
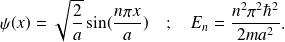
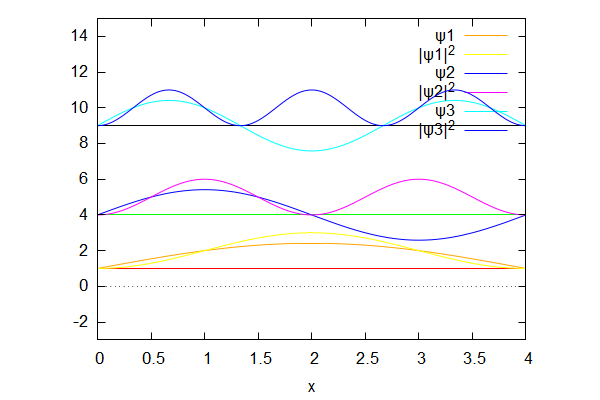
Sur la figure suivante, sont représentées les trois premiers niveaux ainsi que les fonctions d'onde et les densités de probabilité correspondantes.
Remarque :
L'énergie est quantifiée : seuls les niveaux correspondant à des valeurs entières de
 sont accessibles à la particule.
sont accessibles à la particule.
L'énergie la plus basse n'est pas nulle ! Ce qui n'a pas d'équivalent en mécanique classique. Cela s'explique par le principe d'incertitude.
Lorsque la largeur du puits augmente, les niveaux se resserrent et aux grandes valeurs ils forment un continuum comme en mécanique classique. L'effet quantique disparaît.