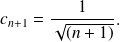Méthode des Opérateurs
Soit le hamiltonien
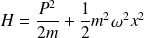 et le commutateur
et le commutateur
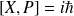
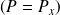 .
.
Les solutions propres vérifient :
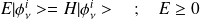 .
.
On introduit les opérateurs:

et les opérateurs :
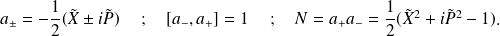
Remarque :
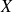 et
et
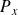 sont hermitiens
sont hermitiens
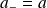 et
et
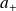 sont adjoints l'un de l'autre :
sont adjoints l'un de l'autre :
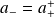 et
et
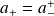
On peut récrire
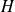 en fonction de
en fonction de
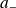 et de
et de
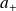 :
:
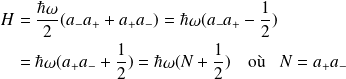
de plus, on a :
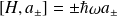 .
.
Soit
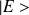 un ket propre associé à la valeur propre
un ket propre associé à la valeur propre
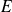 :
:
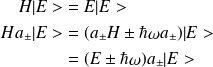
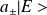 est aussi ket propre de
est aussi ket propre de
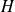 associé à la valeur propre
associé à la valeur propre
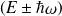 .
.
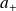 incrémente
incrémente
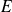 de
de
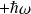 : c'est l'opérateur de création
: c'est l'opérateur de création
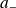 décrémente (réduit)
décrémente (réduit)
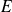 de
de
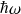 : c'est l'opérateur d'annihilation
: c'est l'opérateur d'annihilation
Si
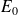 désigne la plus petite des valeurs propres associée à
désigne la plus petite des valeurs propres associée à
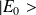 , alors on doit avoir :
, alors on doit avoir :
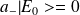 .
.
En agissant sur
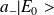 par
par
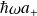 on a :
on a :
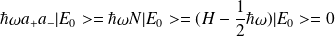 .
.
D'où on déduit que
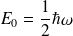 .
.
Remarque : On voit d'après ce résultat que l'énergie du niveau le plus bas n'est pas nulle mais vaut
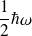 . Ce résultat est contraire à ce que l'on a en mécanique classique où l'énergie la plus basse est
. Ce résultat est contraire à ce que l'on a en mécanique classique où l'énergie la plus basse est
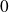 .
.
Par applications successives de
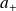 à
à
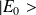 , on a :
, on a :
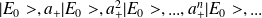
avec
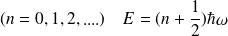 .
.
* Expression de
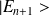 :
:
Soit
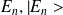 et
et
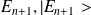
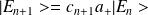 et
et
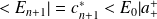
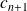 sont des coefficients de normalisation.
sont des coefficients de normalisation.
Comme on a:
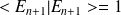 et
et
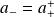 on a :
on a :
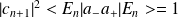
or
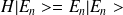 avec
avec
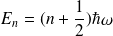
et comme
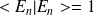 on tire :
on tire :