Définitions
Soit
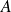opérateur linéaire et hermitien tel que :
.
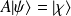est un opérateur associé à une transformation unitaire si pour deux états :
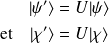
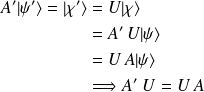
Or, d'après les propriétés de
, on a :
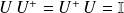
et, par conséquent,
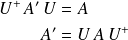
Propriétés :
(i)
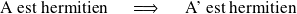
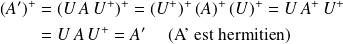
(ii) La forme des équations reste la même :
Si
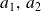sont des constantes et
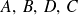des opérateurs tel que :
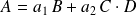, on a :
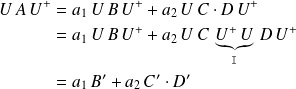
Si
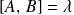, on a :
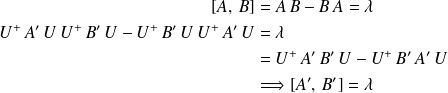
(iii) les valeurs propres de
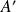sont les mêmes que celles de
:
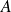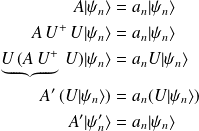
(iv)
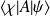reste inchangé par une transformation unitaire :
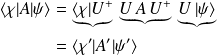
Corollaire : la valeur moyenne reste inchangée par une transformation unitaire.
si
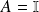, alors
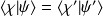
et si
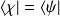, alors le produit scalaire et la norme sont des invariants.
L'importance de ce résultat fait qu'un problème dynamique peut être plus facilement résolu si on trouve une transformation unitaire adéquate permettant d'obtenir un nouvel ensemble de fonctions et d'opérateurs.
Soit un système à 1-D décrit par l'état
.
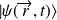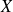représente l'opérateur position et
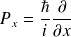, l'opérateur impulsion.
La transformée de Fourier est une transformation unitaire :
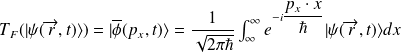
On peut écrire cette expression sous la forme :
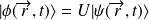. Il s'agit bien d'une trasformation unitaire (on a vu, que la transformée de Fourier conservait le produit scalaire - et donc, la norme).
La transformée inverse s'écrit :
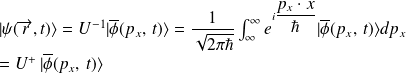
On vérifie aisément que :
.
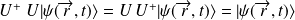l'opérateur intégral
est unitaire et on retrouve la propriété de conservation de la norme :
.
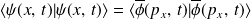