Transformations Infinitésimales
Si on peut trouver un réel
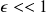tel que l'opérateur
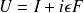, où
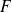est un opérateur hermitien, alors
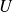est dit infinitésimal.
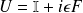
En effet, en combinant les deux relations et (et en s'arrétant au premier ordre du développement), on écrit :
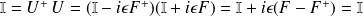
Par conséquent,
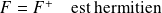
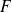est dit générateur de la transformation infinitésimale et
son paramètre.
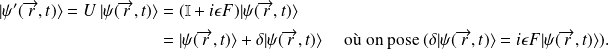
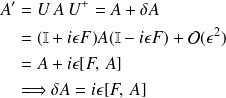
Applications
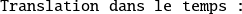
Soit un état
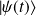. On considère l'opérateur
et
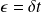, l'opérateur transformation unitaire
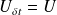prend la forme :
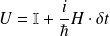
Sachant que
,
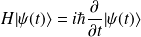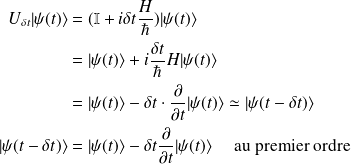
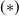l'application de
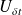à
donne l'état
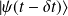qui est une translation de l'état
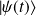dans le temps de la quantité
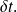
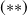
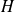est le générateur de la transformation infinitésimal associée à la translation dans le temps.
Remarque :
La forme de
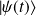est conservée (simple translation de
).
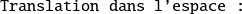
Dans ce cas, on prend pour
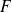l'opérateur
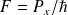et
.
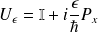Sachant que
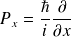, on a :
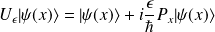
Or, un développement de la fonction d'onde autour de la position
s'écrit :
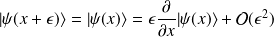
En combinant ces deux écritures, on obtient :
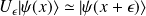
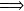il s'agit d'une translation de
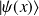de la quantité
.
{\rem{ Partant de
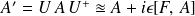, si on prend
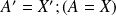on a :
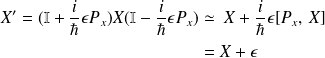
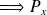est le générateur de la transformation infinitésimale de translation spatiale.
