Connexion entre Mécanique Classique et Mécanique Quantique
Soit
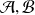deux variables dynamiques dépendant des coordonnées généralisées
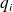, des moments
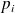et du temps
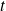. Dans ce qui suit, on utilise indifféremment
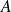et
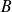pour désigner la grandeur dynamique ou l'opérateur associé. En mécanique classique on définit le crochet de Poisson par :
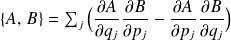
Et puisque les
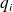sont indépendants de
:
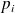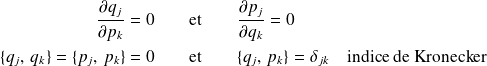
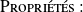
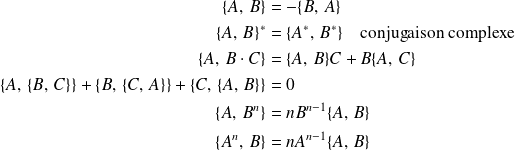
La dérivée totale, par rapport au temps, de
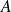s'écrit :
Or, on utilisant les équations de Hamilton :
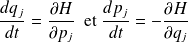
où
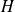est le hamiltonien et
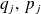les variables conjuguées, il vient,
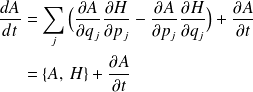
résultat à comparer avec :
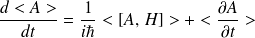
ce qui donne la relation entre le crochet de Poisson et le commutateur : (après avoir appliqué le principe de correspondance en associant à la variable dynamique
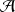l'observable
).
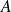Si
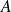ne dépend pas explicitement du temps
:
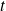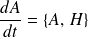
Et si, de plus,
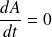ou
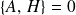alors,
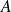est une constante du mouvement.
Exemple :
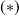Calcul de
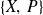, avec,
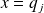et
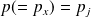
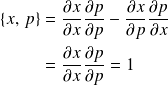
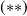le calcul du commutateur des deux observables
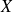et
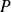donne :
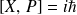
soit, en regroupant les deux résultats :
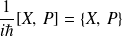
la relation est donc vérifiée.
