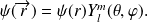Rappels
Soit un système formé de deux particules, de masses
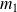 et
et
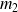 , interagissant via un potentiel indépendant du temps (
, interagissant via un potentiel indépendant du temps (
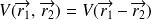 ). Le hamiltonien du système s'écrit :
). Le hamiltonien du système s'écrit :
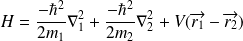
L'évolution dans le temps de l'état de ce système est donnée par :
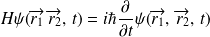
On peut adopter le système de coordonnées liées au centre de masse (de masse
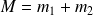 ) :
) :
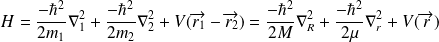
On a alors,
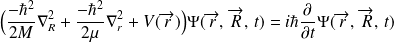
Cette équation peut être séparée de la manière suivante :
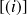 le potentiel étant indépendant du temps, on écrit :
le potentiel étant indépendant du temps, on écrit :
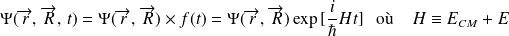
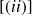 la partie spatiale
la partie spatiale
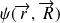 peut être séparée aussi sous la forme de produits de fonctions des coordonnées du centre de masse (CM)\ref{Figure-CM},
peut être séparée aussi sous la forme de produits de fonctions des coordonnées du centre de masse (CM)\ref{Figure-CM},
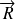 , et relatives,
, et relatives,
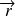 :
:
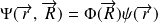
tel que :
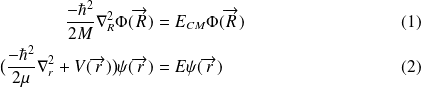
La première équation est analogue à l'équation de Schrödinger pour une particule libre de masse
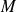 . La seconde équation, est l'équation de Schrödinger pour une particule de masse
. La seconde équation, est l'équation de Schrödinger pour une particule de masse
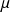 placée dans un potentiel
placée dans un potentiel
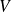 et,
et,
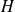 correspond à énergie totale (deux particules), i.e.
correspond à énergie totale (deux particules), i.e.
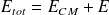 .
.
Le problème à deux corps est ramené à celui de deux problèmes à un corps : le centre de masse considéré comme une particule libre, et la particule de masse
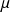 se déplaçant dan le potentiel
se déplaçant dan le potentiel
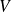 . Le choix du système de coordonnées lié au centre de masse permet de s'affranchir des ses coordonnées relatives : on peut alors rechercher les solutions de l'équation en (
. Le choix du système de coordonnées lié au centre de masse permet de s'affranchir des ses coordonnées relatives : on peut alors rechercher les solutions de l'équation en (
 ) :
) :