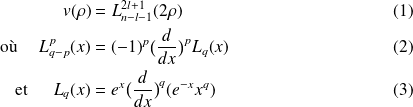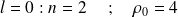Fonction d'Onde Radiale dans le cas d'un Hydrogénoïde
Le potentiel
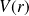 s'écrit :
s'écrit :
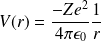 .
.
En posant,
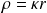 et
et
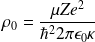 , l'équation de Schr\"odinger devient :
, l'équation de Schr\"odinger devient :
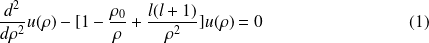
Et on a toujours un comportement asymptotique de
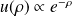 lorsque
lorsque
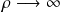 .
.
Lorsque
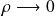 (i.e.
(i.e.
 ), on a
), on a
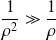 et l'équation admet alors une solution asymptotique vérifiant :
et l'équation admet alors une solution asymptotique vérifiant :
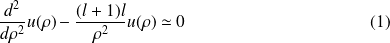
et s'écrivant :
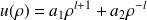
pour
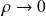 , le deuxième terme diverge, par conséquent
, le deuxième terme diverge, par conséquent
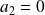 .
.
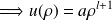
La solution de l'équation doit ainsi avoir un comportement identique aux asymptotes pour
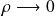 et
et
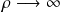 . On définit la fonction :
. On définit la fonction :
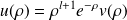
Après substitution dans l'équation de Schrödinger, on obtient :
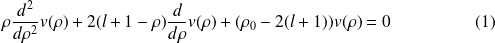
On recherche une solution telle que
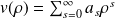 et on reporte encore dans l'équation, (\ref{Eq:v}), le but étant de trouver les coefficients
et on reporte encore dans l'équation, (\ref{Eq:v}), le but étant de trouver les coefficients
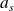 . On trouve la relation de récurrence :
. On trouve la relation de récurrence :
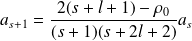
ainsi, en partant d'une valeur
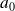 , il sera possible d'obtenir tous les coefficients du développement
, il sera possible d'obtenir tous les coefficients du développement
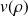 , et, par suite, la solution
, et, par suite, la solution
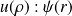 sera déterminée totalement.
sera déterminée totalement.
Dans le cas
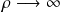 , (
, (
 est grand) on a :
est grand) on a :
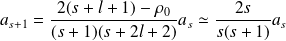
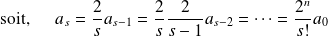
et on a alors,
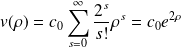
et
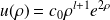
Mais, pour
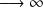 ,
,
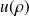 diverge, ce qui implique que les termes
diverge, ce qui implique que les termes
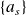 soient en nombre fini : au delà d'une valeur de
soient en nombre fini : au delà d'une valeur de
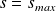 , les
, les
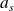 sont nuls. (
sont nuls. (
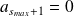 ).
).
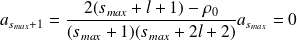
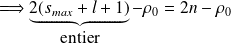
Ainsi
 et, en reportant les expressions de
et, en reportant les expressions de
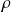 ,
,
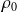 et
et
 , on a :
, on a :
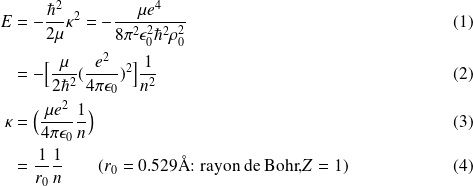
les états propres s'écrivent finalement sous la forme :
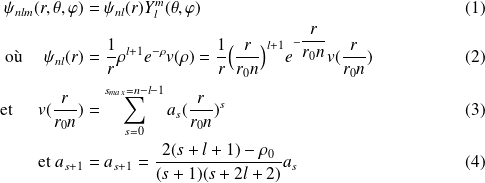
Pour l'état fondamental
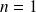 \\
\\
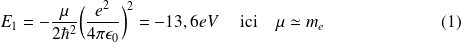
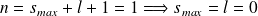 et
et
 . L'état propre correspondant est donc :
. L'état propre correspondant est donc :
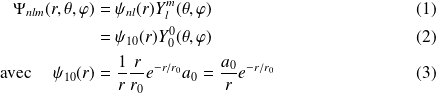
Remarque :
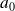 est un coefficient du développement de
est un coefficient du développement de
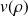 : le seul non nul. Avec la condition de normalisation :
: le seul non nul. Avec la condition de normalisation :
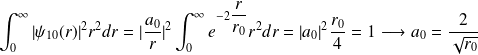
Soit :

Pour
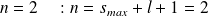
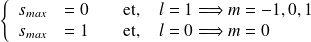
La dégénérescence totale est :
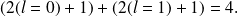
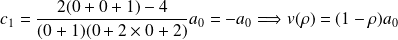
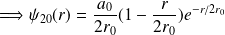
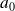 est déterminé à partir de la condition de normalisation.
est déterminé à partir de la condition de normalisation.
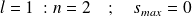 , on a un seul coefficient (c'est
, on a un seul coefficient (c'est
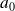 ).
).
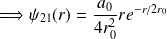
Pour une valeur donnée de
 , la dégénérescence sera
, la dégénérescence sera
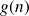 . Les valeurs permises pour
. Les valeurs permises pour
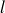 sont :
sont :
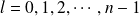 , et pour chaque valeur de
, et pour chaque valeur de
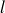 , il y a
, il y a
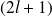 valeurs permises pour
valeurs permises pour
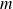 (projection de
(projection de
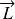 sur
sur
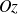 )
)
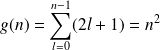
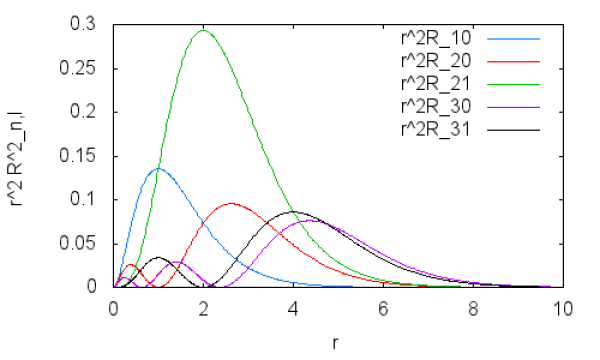
Une écriture des fonctions
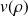 , sous forme de polynômes de Laguerre avec des relations de récurrence, donne :
, sous forme de polynômes de Laguerre avec des relations de récurrence, donne :