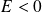Particule dans un Champ Central
On considère un champ central symétrique et qui s'annule à l'infini. L'équation correspondante est :
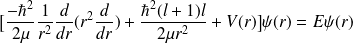
où on considère le laplacien en coordonnées sphériques,
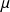la masse réduite de la particule et
la coordonnée relative. Tout se passe comme s'il s'agissait d'une particule de masse
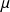en mouvement soumise à un potentiel effectif
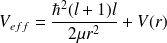. Le premier terme correspond à un potentiel centrifuge qui rend répulsif
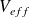aux courtes distances.
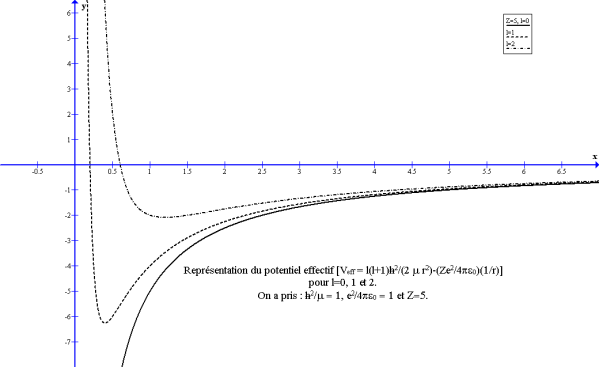
On récrit l'équation sous la forme :
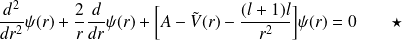
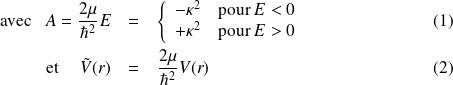
On effectue un changement intermédiaire :
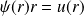tel que (
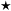) devient :
Remarque :
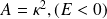: les solutions correspondent à des états liés. Par contre,
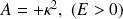le spectre est continu.
On distingue donc deux cas :
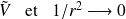pour
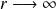, l'équation (\ref{Eq-Sch}) devient :
les solutions sont de la forme :
Le comportement des solutions est celui d'une superposition d'une onde sphérique entrante (incidente) et une autre sortante (réfléchie). Ces solutions se retrouvent dans l'étude de la diffusion d'une particule par un champ créé par un potentiel. %
La solution s'écrit dans ce cas :
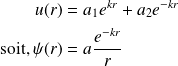
car la condition,
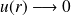lorsque
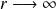, impose le choix de la fonction :
.
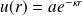Remarque :
la probabilité de présence de la particule est proportionnelle au carré du module de
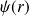, on voit que
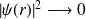lorsque
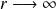: la particule est localisée dans une région de l'espace
.
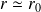