Fonction d'Onde - Etat - Espace des Etats
Définition : Postulat 1
A un ensemble de systèmes physiques on peut, dans certains cas, associer une fonction d'onde, notée
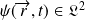, ou encore une fonction de l'espace des états notée
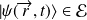, qui contient toutes les informations sur cet ensemble.
Si on a
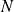systèmes identiques dans le même état
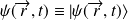, la fonction d'état associée à cet ensemble (
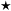)dépend, dans l'espace de configuration, de
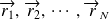et du temps
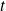. On a :
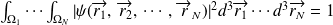
On définit la densité de probabilité (de position) de trouver, à l'instant
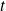, le système
dans le volume
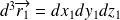autour de
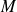, le système
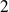dans le volume
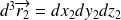, etc. par,
.
(
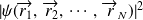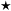) Comme il s'agit d'un système à
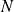particules identiques et indépendantes, la fonction
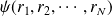s'écrit en fait comme un produit tensoriel des fonctions individuelles
.
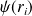Il s'agit, en effet, de situations où les particules composant le système sont toutes identiques et préparées dans le même état. Dans les autres cas, plus généraux, on aura recourt à la matrice densité.
Définition : Postulat 2
Les états dynamiques d'un système sont linéairement superposables.
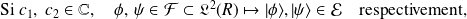alors
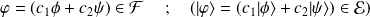
Fonction d'onde - Espace des états
On définit le conjugué hermitien :
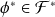de
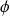, où
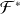désigne le dual de
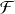, (auquel on associe, en notation de Dirac, le bra
),
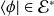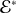étant le dual de
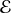et
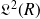l'espace des fonctions de carré sommable.
On définit le produit scalaire :
à tout
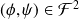, pris dans cet ordre, on associe un nombre complexe noté
, (
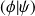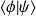en notation de Dirac), tel que :
