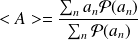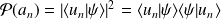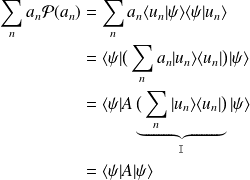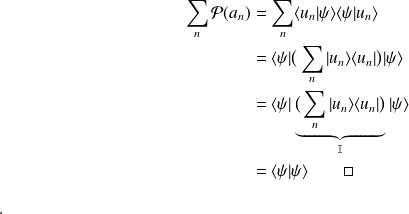Opérateurs
Définition : Postulat 3
chaque variable dynamique on associe un opérateur linéaire.
opérateur tel que, si
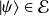, alors,
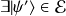tel que :
.
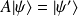est linéaire si (pour
):
.
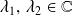Ce principe permet, par correspondance, d'associer à une variable dynamique classique,
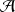, un opérateur
qui, par son action sur le vecteur d'état, rend compte de la mesure de cette même variable.
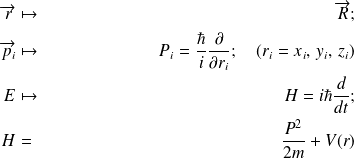
Exemple :
.
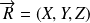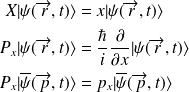
Opérateur adjoint, opérateur hermitien
et
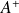sont adjoints si :
,
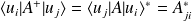( ou bien, si
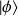et
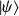sont deux états, on a :
).
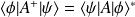Si
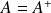, alors
et
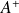sont hermitiens, (
est dit autoadjoint).
Soit
un opérateur. On note, dans la base discrète :
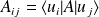; et dans la base continue
.
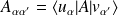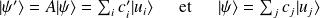
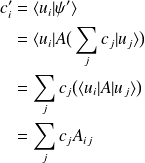
Commutation entre opérateurs
On définit le commutateur de deux opérateurs par :
.
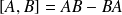Remarque : On définit aussi l'anti-commutateur
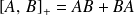, cependant, on s'intéresse particulièrement au commutateur parce qu'on peut établir, comme on le verra plus loin, une relation avec le crochet de Poisson en physique classique.
Soit
et
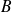deux opérateurs qui commutent entre eux, i.e.
,
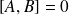si
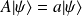alors
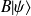est ket propre de
associé à la même valeur propre
:
,
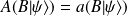si
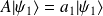et
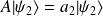, avec
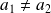, alors
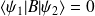
Remarque : s'il existe une base formée des kets propres de
et
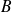alors commutent.
Observables
Une observable est un opérateur hermitien tel que l'on peut former avec ses vecteurs propres une base de l'espace des états
.
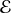Remarque : si
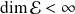, cela est vrai. Si
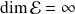, ce n'est pas toujours vrai.
Soit
un opérateur hermitien ayant pour valeurs propres
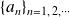et pour états propres
.
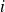représente le degré de dégénérescence de la valeur propre
.
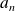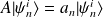
Si
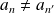, on a :
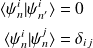
Par définition :
Soit
un opérateur hermitien.
est une observable si
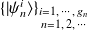
forme une base. Dans ce cas, la relation de fermeture prend la forme suivante :
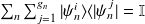
Ensemble complet d'observables qui commutent
Si
et
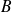sont deux observables tel que
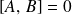et, si,
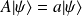, alors :
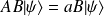
Si
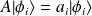, alors :
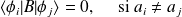
Définition :
Un ensemble d'opérateurs hermitiens
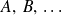forme un E.C.O.C. s'ils commutent deux à deux et si leurs vecteurs propres communs forment un ensemble complet et non dégénéré, i.e. chaque vecteur de la base commune est défini d'une manière unique par la donnée des valeurs propres de ces observables.
Remarque : Un E.C.O.C. très important est celui qui contient le hamiltonien
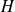. En effet, dans ce cas, les grandeurs dynamiques associées aux différentes observables de l'E.CO.C. peuvent être mesurées simultanément, sont des constantes du mouvement et, donc, indépendantes du temps.
Représentation matricielle
Un opérateur peut être associé à une matrice :
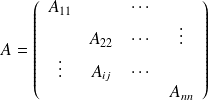
Si
est hermitien (i.e.
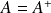) alors,
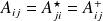, on en déduit que les
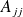sont réels.
Fonctions d'opérateurs
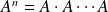, par analogie avec les polynômes, on peut développer une fonction
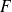d'un opérateur sous la forme :
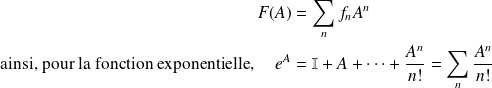
si
est hermitien,
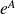l'est aussi.
Soit
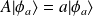, on a :
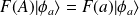
Si
,
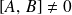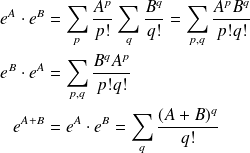
Si
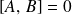, alors,
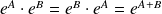
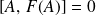, en effet,
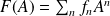
Trace d'un opérateur
La trace d'un opérateur s'exprime par :
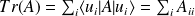
( c'est un invariant de
)
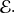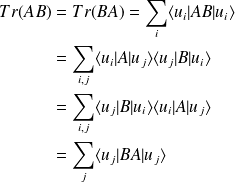
On montre de la même manière, pour trois ou plus d'opérateurs, que l'on a :
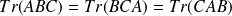
Définition : Mesure
Notion de mesure
Soit
associée à la variable dynamique
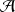. La mesure d'une grandeur physique ne peut donner comme résultat que l'une des valeurs propres de l'observable correspondante. L'ensemble des valeurs
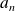est dit spectre de
. Il peut être discret ou continu.
-
est une observable, i.e.
est hermitien et ses vecteurs propres constituent une base,
l'équation aux valeurs propres s'écrit : (
)
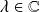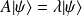ou encore (
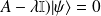
et en écriture matricielle :
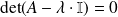
si, à la valeur propre
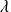sont associés
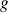vecteurs propres, alors,
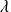est de dégénérescence
(
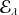est le sous-espace associé à
).
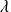E.C.O.C. (Ensemble Complet d'observables qui commutent).
Définition : Postulat
Soit un système dans l'état
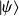normé. Soit
l'observable associée à la grandeur physique
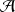. La probabilité d'obtenir la valeur
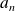de
est :
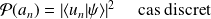
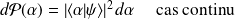$$
Remarque :
cas non dégénéré :
soit
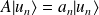et
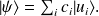
\par
La probabilité d'obtenir la valeur propre
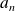est donnée par :
.
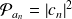cas dégénéré :
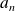est
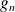fois dégénérée :
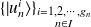
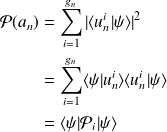
où
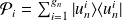définit le projecteur sur le sous-espace
.
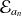si |
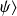n'est pas normé :
.
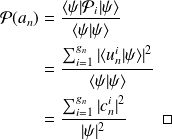Définition : Postulat : Valeur Moyenne d'un Opérateur
Si une série de mesures d'une variable dynamique
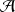est effectuée, sur un ensemble de systèmes identiques, décrit par
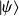, la valeur moyenne de cette variable dynamique est :
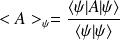
Soit
un opérateur ayant un spectre discret non dégénéré :
.
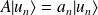\par
Remarques :
définition statistique de
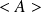(la probabilité est donnée par le rapport du nombre de cas favorables au nombre de cas possibles) :
