Evolution dans le Temps
Définition : Postulat
L'évolution dans le temps de
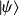 , état décrivant un système donné, est déterminée par l'équation de Schrödinger dépendant du temps :
, état décrivant un système donné, est déterminée par l'équation de Schrödinger dépendant du temps :
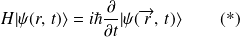
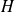 est l'opérateur hamiltonien associé à l'énergie totale du système.
est l'opérateur hamiltonien associé à l'énergie totale du système.
Remarque :
(*) est une équation différentielle de premier ordre en
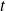 : connaissant
: connaissant
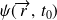 , il est possible de déterminer
, il est possible de déterminer
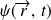 pour
pour
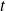 quelconque.
quelconque.

On introduit l'opérateur évolution
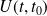 qui vérifie les propriétés et équations suivantes :
qui vérifie les propriétés et équations suivantes :
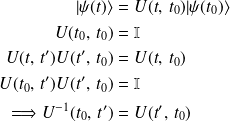
On reconnaît les propriétés de groupe.
De plus
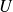 vérifie l'équation :
vérifie l'équation :
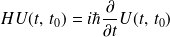
La conservation de la probabilité nécessite :
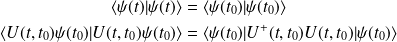
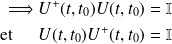
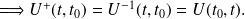
Par conséquent,
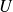 est un opérateur unitaire.
est un opérateur unitaire.
Remarque :
Si
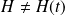 (le système est conservatif), une solution qui satisfait la condition initiale
(le système est conservatif), une solution qui satisfait la condition initiale
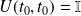 prend la forme suivante:
prend la forme suivante:
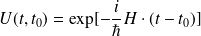
et la solution formelle de l'équation de Schrödinger dépendant du temps s'écrit :
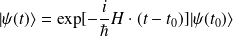 .
.

Variation de la valeur moyenne
Soit
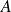 une observable et
une observable et
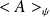 la valeur moyenne de
la valeur moyenne de
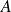 dans l'état normé
dans l'état normé
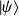 .
.
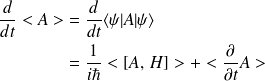
Si
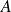 ne dépend pas de
ne dépend pas de
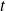 , et si
, et si
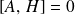 , alors l'observable
, alors l'observable
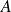 est une constante du mouvement.
est une constante du mouvement.
Exemple
Soit une particule dans un potentiel ne dépendant pas du temps, de hamiltonien
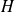 tel que :
tel que :
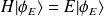 ,
,
et
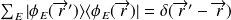 (i.e.
(i.e.
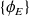 est une base propre).
est une base propre).
On suppose que l'état, à un instant
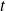 , s'écrit dans la base propre comme suit :
, s'écrit dans la base propre comme suit :
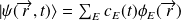
On a de plus :
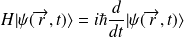
Soit, en utilisant l'opérateur évolution dans le temps et la relation de fermeture dans la base des états propres
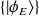 :
:
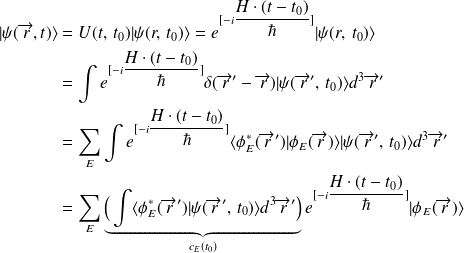
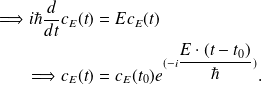
On retrouve le principe de superposition que dans le cas d'un potentiel indépendant de
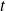 , les états stationnaires
, les états stationnaires
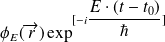 sont des solutions particulières de l'équation de Schrödinger dépendant de
sont des solutions particulières de l'équation de Schrödinger dépendant de
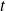 .
.
Analogie avec la mécanique classique (équation de Hamilton)
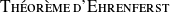
Pour
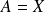 , et pour un système décrit par le hamiltonien
, et pour un système décrit par le hamiltonien
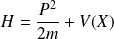 ,
,
on a
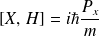 et
et
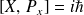 , ce qui donne :
, ce qui donne :
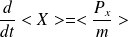
Pour
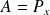 , on obtient :
, on obtient :
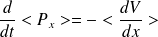
Il y a analogie avec la mécanique classique (équation de Hamilton) :
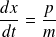 et
et
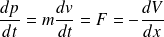 (la force
(la force
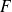 dérive du potentiel
dérive du potentiel
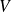 ).
).
Mesure et relations d'incertitude
Si deux observables associées à deux grandeurs (dynamiques) physiques commutent, il est possible de mesurer ces deux grandeurs simultanément.
Si
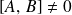 , les mesures obéissent à la condition d'incertitude :
, les mesures obéissent à la condition d'incertitude :
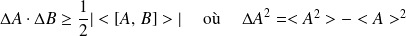
Si
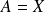 et
et
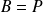 , sachant que
, sachant que
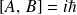 , on obtient :
, on obtient :
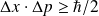 .
.





