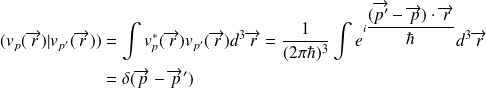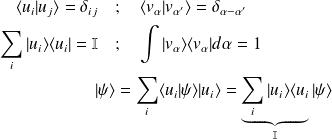Bases de F
(i) Base discrète
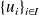
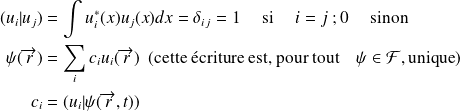
et
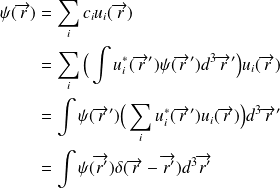
On a défini la relation de fermeture :
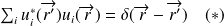
Cette relation exprime le fait que l'ensemble des fonctions
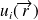est complet, i.e. toute fonction d'onde peut être développée comme une combinaison linéaire des
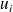. Il en est de m\^eme pour l'ensemble formé des états propres d'une observable qui sera traité plus loin.
Remarque : si
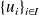constitue une base de
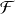, elle satisfait cette relation
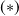et réciproquement -( il y a équivalence).
(ii) base continue
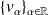
Remarque :
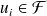, par contre,
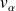n'appartient pas forcément à
.
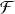si
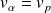, il s'agit d'ondes planes et de paquets d'ondes :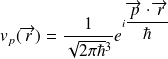
transformée de Fourier :
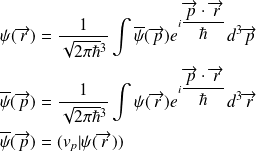
relation de fermeture :
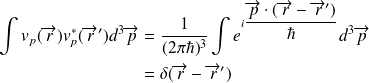
relation d'orthonormalisation des vecteurs propres :
