Définition Générale du Moment Cinétique
Définition :
En mécanique classique, une particule de masse
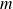et de quantité de mouvement
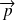procède un moment cinétique
(
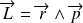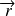: position par rapport à l'origine fixe
)
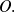En mécanique quantique, on utilise le principe de correspondance : l'opérateur associé à
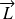est :
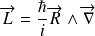où
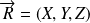représente l'opérateur position.
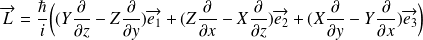
En coordonnées sphériques :
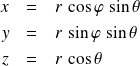
On obtient alors :
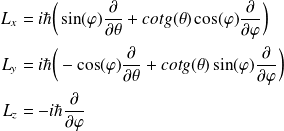
Et
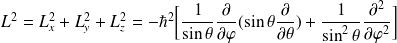
Etant donné les relations de commutation entre les opérateurs
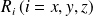et
:
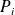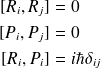
On calcule les commutateurs entre les composantes
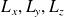de
:
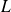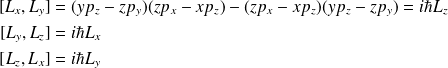
Ces relations sont résumées dans une écriture vectorielle :
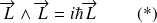
Remarque :
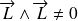car les composantes ne commutent pas entre elles !
On a aussi, (puisque
),
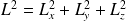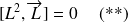
Les deux relations
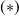et
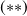sont caractéristiques d'un moment cinétique.
En effet, en mécanique quantique, on appelle moment cinétique tout opérateur
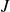(opérateur vectoriel) vérifiant les deux relations :
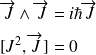
Ou encore :
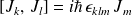
où
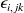désigne le symbole de Levi-Civita pour les permutations des indices
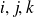tel que :
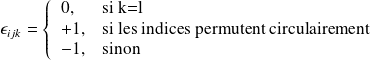
Remarque : Si on considère un système isolé formé de
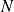particules identiques (sans structure interne, i.e. sans spin) tel que, si
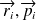représentent, respectivement, les coordonnées et la quantité de mouvement de la i-ème particule, son moment angulaire sera
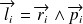et le moment total des
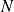constituants est donné par :
.
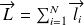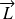vérifie alors les relations ci-dessus.
