Moment Cinétique et Rotations dans l'Espace
Soit un système isolé. L'espace étant isotrope (toutes les directions sont équivalentes), une rotation appliquée à ce système doit conserver ses propriétés physiques.
Ainsi, l'application de la rotation
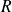à l'état
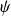décrivant le système donne l'état
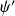tel que :
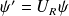où
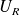est un opérateur unitaire.
On a :
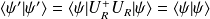
la norme est conservée et, de façon générale, l'amplitude
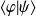est conservée sous la rotation.
De même,
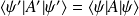
avec
.
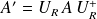Remarque : en particulier :
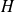se conserve (le système étant isolé
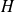est un invariant) :
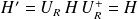ou encore
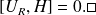
Pour trouver une forme explicite de
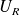, on considère une particule (sans structure interne) décrite à un instant
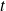par
.
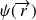Sous l'action de
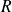, le vecteur position
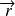se transforme en
:
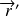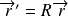et on a
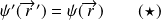
Or, nous avons aussi :
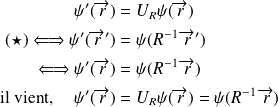
(Il s'agit en fait de la définition de la bijection :
.)
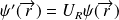Pour aborder la nature du moment angulaire nous allons, à travers une rotation infinitésimale, et suivant le raisonnement sur les opérateurs unitaires correspondants, établir la relation entre les deux.
Soit une rotation infinitésimale, d'angle
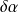, positive suivant l'axe
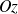. L'opérateur infinitésimal associé est
.
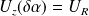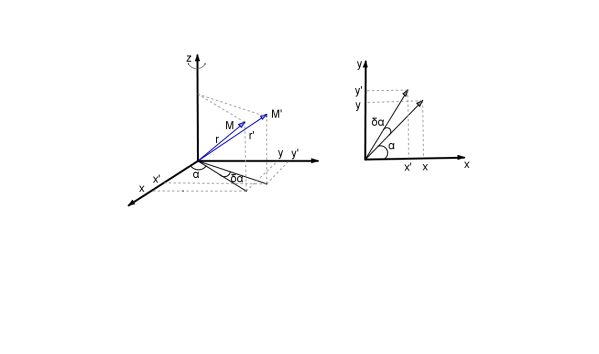
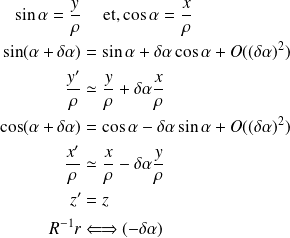
On a alors :
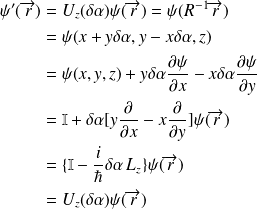
Comme
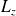est hermitien (
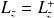), il est le générateur de la rotation infinitésimale de paramètre
.
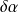Il en est de même pour
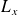et
:
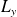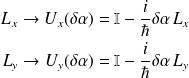
Remarques :
1/ de manière plus générale, si la rotation est effectuée suivant un axe de vecteur unitaire
:
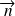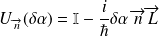
2/ A moins qu'elles n'aient lieu par rapport au même axe, les rotations ne commutent pas entre elles (en général) :
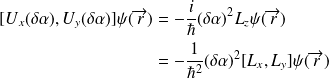
d'où on déduit :
.
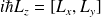