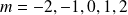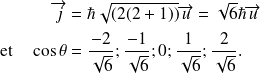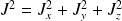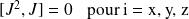Formalisme du Moment Cinétique
Le moment cinétique vérifie les relations :
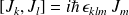et
.
.
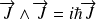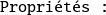
Et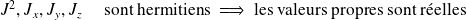ats et valeurs propres de
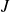
Comme
,
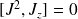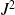et
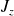peuvent être diagonalisés séparément. (On aurait tout aussi bien pu choisir
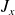ou
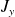au lieu de
).
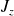Soit
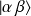le ket propre commun à
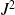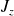et
et
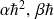les valeurs propres associées respectivement.
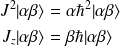
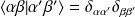
On introduit les opérateurs de montée et de descente :
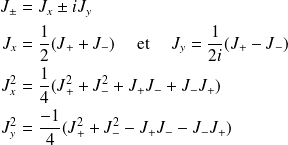
On montre les relations suivantes :
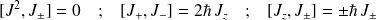
et on a les relations suivantes pour
:
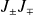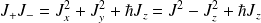
et
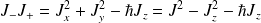
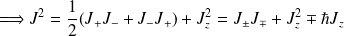
(1-) On fait agir
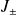sur
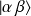. Sachant que
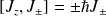, on a :
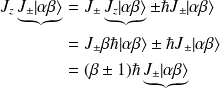
Ainsi,
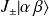sont des kets propres de
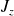associés aux valeurs propres
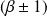respectivement.
(2-) de même on a :
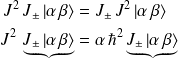
De (1-) on infère que l'action de
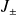sur
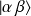produit un état
:
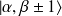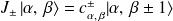
Comme
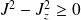, on en déduit qu'il y a, pour une valeur de
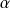(valeur propre de
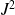), une valeur limite pour
.
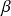En effet :
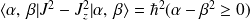
soit,
.
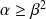Et pour
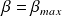, l'état correspondant ne peut être élevé par l'action de
.
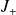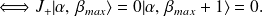
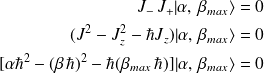
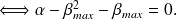
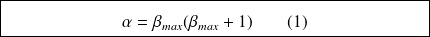
Après
opérations successives de
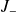sur
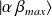, on arrive à
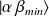tel que :
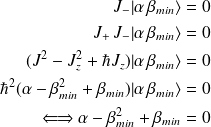
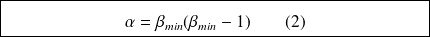
De
et
on conclut que
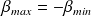et pour atteindre
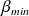, on a dû appliquer
:
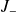
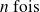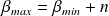
soit :
.
(
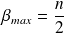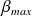peut ainsi être soit entier, soit demi-entier.)
On note alors :
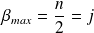et
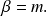
Soit,
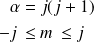
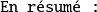
D'après ce qui précède, les valeurs propres et vecteurs propres des observables
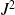et
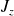sont donnés par :
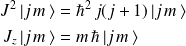
avec
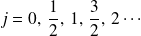et
.
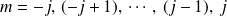Ainsi, pour
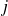donné, nous avons
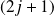valeurs de
.
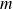Les spectres de
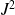et
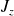sont discrets et la condition d'orthonormalité est :
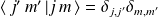
On se propose maintenant d'exprimer l'action de
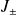sur les états
:
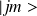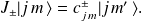
Calcul pour
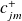et
:
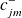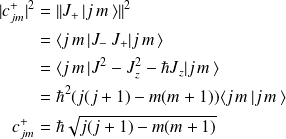
Calcul pour :
un calcul analogue donne :
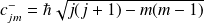
Il s'en suit :
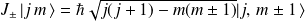
A partir de ces relations, on calcule l'action des opérateurs
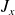et
:
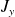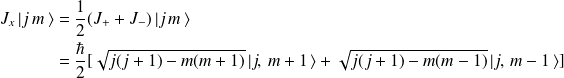
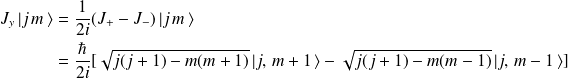
D'où on déduit les résultats suivants :
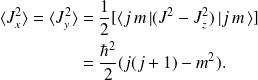
Représentation matricielle
,
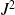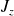commutent, l'ensemble des vecteurs communs peut être pris comme base. (base discrète, orthonormale et complète).
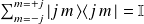
Les matrices associées à
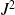et
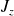sont diagonales dans
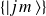(leur base commune) :
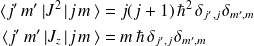
Les éléments diagonaux pour
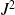et
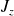sont respectivement :
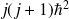et
.
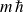Pour les opérateurs
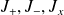et
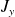, les éléments de matrice associée s'écrivent :
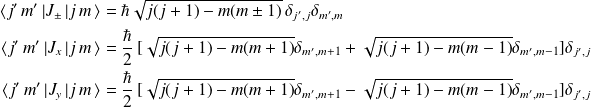
On considère le cas où
.
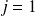- Trouver les matrices représentant
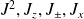et
.
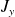Pour
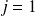, les valeurs possibles pour m sont
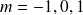. Les vecteurs de la base sont :
.
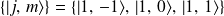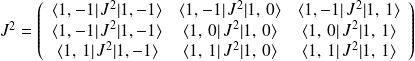
Or, on a
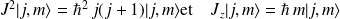
La matrice représentant
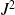s'écrit alors :
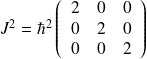
Un calcul similaire donne pour
:
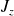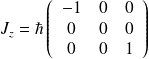
On remarque que
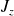est diagonal et les éléments diagonaux sont les valeurs propres
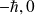et
.
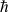Représentation standard
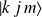
Généralement
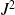et
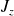ne forment pas un E.C.O.C. à eux seuls. L'ECOC d'un système contiendra d'autres observables
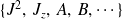et les vecteurs de la base commune dépendra d'autres nombres quantiques :
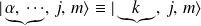où
.
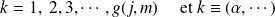Ces états forment une base d'un sous-espace
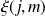tel que
.
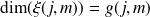L'action de
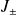(pour
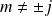) sur ces vecteurs
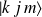donne des vecteurs orthonormées des sous-espaces
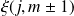de même dimension :
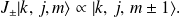
On construit, comme précédemment,
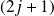sous-espaces
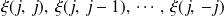de dimensions :
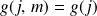(pour une valeur de
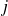donnée et indépendamment de
).
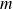L'union de ces sous-espaces pour chacune des valeurs possibles de
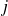constitue l'espace complet des états du système. C'est ce qui définit la base standard :
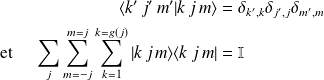
Pour classer les états
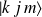et assurer l'invariance d'un sous-espace donné
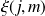sous l'action de
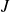, on regroupe ensemble ceux pour lesquels
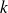et
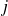ont des valeurs données au lieu du couple
:
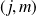Représentation géométrique
La représentation géométrique du moment cinétique
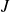(et de sa composante
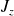) peut être abordée en lui associant (pour une valeur donnée de
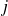) un vecteur de module :
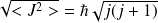
Et dont la projection suivant
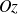est :
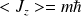
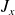et
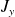ne peuvent être définies séparément :
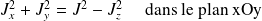
L'extrémité du vecteur
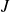associé à
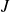décrit (une révolution autour de
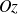) un cercle : base d'un cone de sommet
:
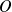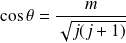
Puisque les valeurs de
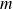sont définies pour un
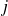par :
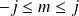, l'angle
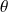est quantifié et , par conséquent, les seules valeurs qu'il peut prendre sont :
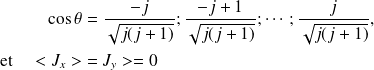
Exemple : pour
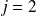, on a les valeurs suivantes de
