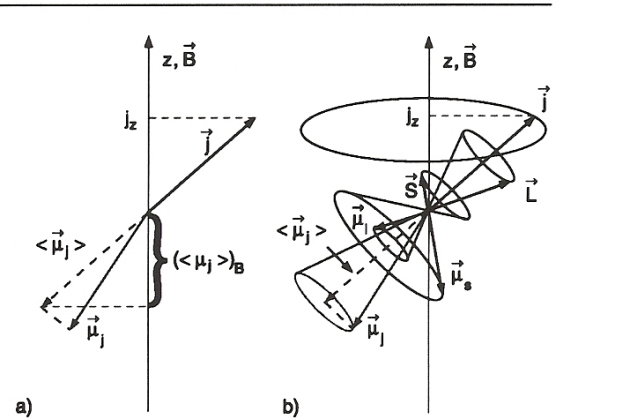
Moment de Spin
Mise en évidence
Stern et Gerlach (1922) font passer des atomes
dans un champ magnétique inhomogène
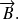Sur l'écran d'observation, le faisceau atomique se scinde en deux.
Les
électrons de l'atome d'argent forment une distribution de charge globalement sphérique et le
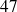ème occupe l'orbitale
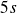(état fondamental).
D'après la mécanique ondulatoire : un électron dans un état défini par le moment orbital
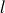, donne en présence d'un champ magnétique
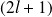niveaux.
Ainsi, l'électron
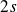de
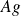devrait donner
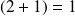niveau (et sur l'écran d'observation : une tache unique). S'il est dans l'état
(
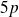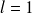), on devrait observer
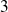taches sur l'écran. Stern et Gerlach n'en obtiennent que deux.
Remarque : Le même résultat est obtenu avec des atomes d'hydrogène.
Interprétation
Goudsmit et Uhlenbeck (1925) postulent que l'électron doit avoir un autre moment lié à un caractère intrinsèque
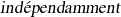des degrés de liberté d'espace : ils l'appellent { spin} par allusion à une rotation propre (intrinsèque) par rapport à l'axe de l'électron.
Remarque:
Comme il n'existe pas d'équivalent en physique classique au spin, celui-ci ne peut être décrit par un opérateur différentiel comme le moment angulaire.
L'énergie d'interaction de ce moment dipolaire avec
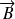est :
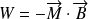
Le hamiltonien total du système devient :
.
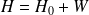Le système (l'électron) subit un couple
,
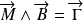et une force :
.
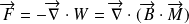On montre que :
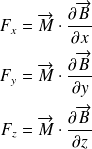
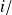si
est uniforme (
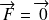), le dipôle est en précession de l'axe de
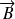à une fréquence
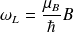, appelée fréquence de Larmor.
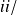si
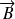est inhomogène,
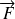est non nulle et agit sur l'électron qui se déplace.
Suivant l'hypothèse de Goudsmit et Uhlenck, on postule que, de la même manière, l'électron a un moment magnétique dipôlaire de spin :
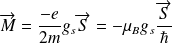
Où
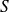désigne le moment de spin et
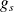un facteur (
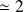), appelé rapport gyromagnétique de l'électron.
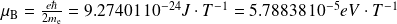désigne le magnéton de Bohr.
Le moment magnétique (dipôlaire) total de l'électron s'écrirait alors :
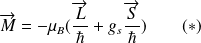
Lorsque l'électron est placé dans un champ magnétique inhomogène, une force, dont la direction et l'intensité dépendent de l'orientation respective du dipôle et du champ, est appliquée. La force tend à aligner le dipôle suivant
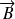et crée un mouvement de précession autour du champ, l'électron est entraîné dans le sens des
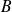croissants. Inversement, si
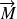et
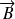sont anti-parallèles, l'électron va dans le sens des
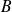décroissants.
D'après
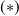, on voit que pour les hydrogénoïdes (
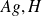, etc.) l'électron étant dans un état
, le dipôle est entièrement dù au spin (en eff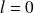et,
et
).
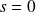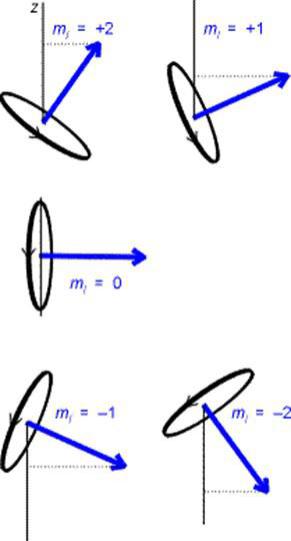
Expérimentalement, les deux taches suggèrent une dégénérescence associée au spin de
:
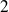En effet, il n'a que deux orientations possibles par rapport à la direction de
.
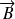Et par analogie avec le moment angulaire, la projection sur l'axe
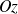de
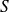(notée
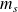) admet deux possibilités, soit :
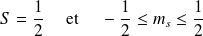
Remarque : Certaines particules ont des spins entiers (
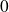: mésons ; photons ;
), ce sont des bosons. D'autres, des spins demi-entiers (
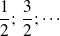), ce sont des fermions.
Le moment de spin satisfait toutes les propriétés du moment cinétique :
Comme pour
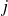, on choisit la composante
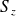et on cherche les vecteurs propres communs à
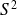et
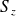tel que :
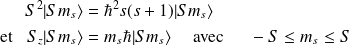
On définit de même les opérateurs d'échelle,
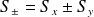vérifiant :
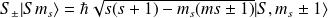
On a aussi :
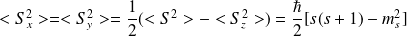
Les états
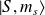vérifient les relations suivantes :
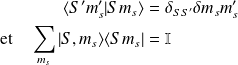
Spin $\frac{1}{2}$ et matrice de Pauli
Pour une valeur de
,
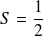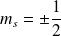. Les états possibles sont alors :
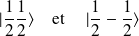, tel que :
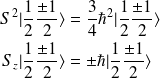
La projection de
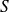sur
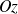se limite aux deux seules valeurs :
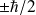
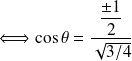
Représentation matricielle de
et
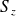
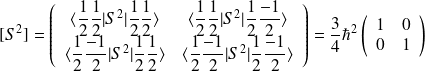
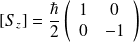
de même pour les opérateurs d'échelle :
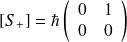
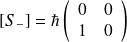
Pour les autres composantes de
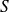, on obtient :
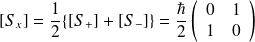
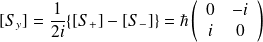
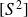est diagonale, les vecteurs propres s'expriment en fonction des vecteurs de la base canonique d'ordre 2 :
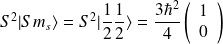
et,
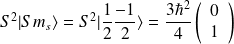
Il est facile de vérifier que ces
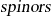forment une base :
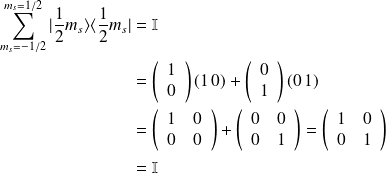
Et :
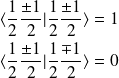
On cherche maintenant à exprimer les vecteurs propres de
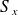et
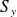, notés respectivement
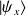et
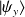, en fonction des spinors : (les états
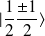ne sont pas des vecteurs propres de
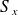et
):
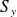Remarques :
-
le moment de spin ne dépend pas des degrés de liberté d'espace, il commute avec
,
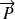et
:
-
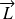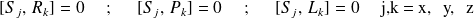
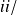l'état
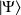décrivant le système avec spin est un produit direct (tensoriel) de l'état
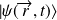(partie spatiale) et de l'état
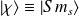de spin :
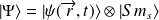
ainsi,
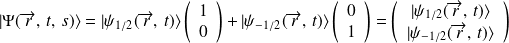
qui définit le vecteur d'état de Pauli.
un état de l'espace
des états de spin s'écrit :
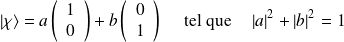
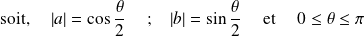
On peut écrire, par suite, une expression plus générale de l'état $| \chi \rangle$ :
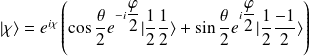
Notons qu'il s'agit d'une écriture unique (aux phases
et
près).
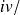Soit le vecteur
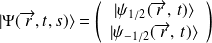
L'application de
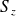à ce vecteur s'exprime comme suit :
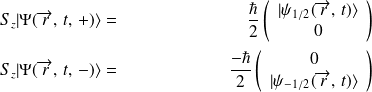
On définit la probabilité de trouver, à l'instant
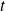et dans l'espace
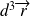, la particule avec un spin
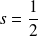par :
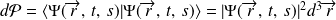
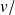soit un vecteur unitaire
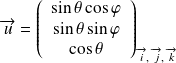,la composante de
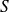dans la direction de
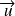est donnée par :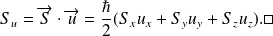
On introduit alors les matrices de Pauli tel que :
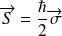
où,
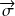désigne l'opérateur vectoriel ayant pour composantes les matrices de Pauli
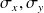, et
.
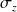Ainsi, par identification avec les matrices obtenues pour
,
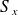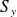et
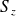, on a :
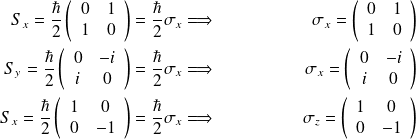
\textsc{ Propriétés des matrices de Pauli}
Les matrices de Pauli vérifient les relations suivantes :
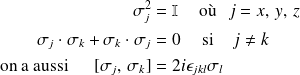
Ces trois relations peuvent être regroupées en une seule :
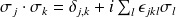
On peut vérifier, en utilisant cette relation, que pour deux opérateurs vectoriels qui commutent avec
, on a :
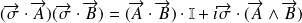
Particulièrement, pour
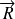et
:
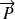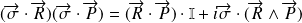
Les matrices de Pauli sont hermitiennes, de trace nulle et leur déterminant égal à
:
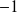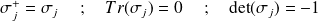
Comme
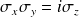et
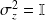, on a
.
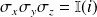