Théorie des Perturbations
Cas Non Dégénérés
Cette méthode est utilisée lorsque le hamiltonien est proche de celui d'un système de hamiltonien
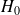 dont on peut calculer les solutions exactes (il peut s'agir du même système dont on connaît les solutions avant l'application d'une perturbation). La différence entre les deux, très petite, est introduite comme une perturbation au hamiltonien non perturbé
dont on peut calculer les solutions exactes (il peut s'agir du même système dont on connaît les solutions avant l'application d'une perturbation). La différence entre les deux, très petite, est introduite comme une perturbation au hamiltonien non perturbé
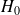 :
:
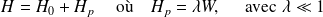
Une telle situation se retrouve dans le cas de systèmes soumis à l'action d'un champ
 ou
ou
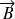 faible.
faible.
Soit
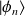 la famille des vecteurs propres de
la famille des vecteurs propres de
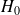 associés aux valeurs propres
associés aux valeurs propres
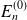 (rappelons-le, supposées jusqu'ici non dégénérées).
(rappelons-le, supposées jusqu'ici non dégénérées).
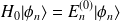
L'idée de base est de considérer les vecteurs et valeurs propres de
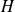 sous forme de développements en puissances de
sous forme de développements en puissances de
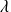 :
:
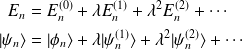
Remarque : pour
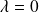 on retrouve les solutions de
on retrouve les solutions de
 .
.

L'équation de Schrödinger s'exprime sous la forme :
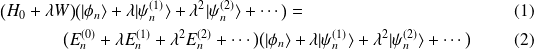
En identifiant les coefficients de même puissance en
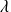 on obtient (en s'arrêtant aux deux premiers termes) :
on obtient (en s'arrêtant aux deux premiers termes) :
ordre
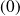 en
en
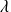 :
:
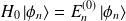
ordre
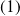 en
en
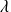 :
:
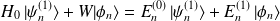
ordre
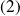 en
en
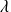 :
:
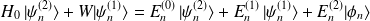
Puisque
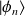 est supposé être proche de
est supposé être proche de
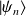 (l'état recherché), on suppose que l'on a
(l'état recherché), on suppose que l'on a
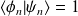 . (En fait,
. (En fait,
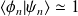 et on normalise pour l'égalité).
et on normalise pour l'égalité).
Soit,
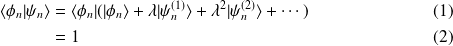
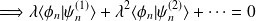
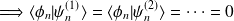
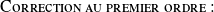
Elle a pour expression, d'après ce qui précède,
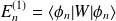
L'énergie perturbée est donc :
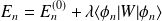
Dans certains cas, le terme
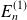 s'annule et on doit déterminer la correction à l'ordre suivant.
s'annule et on doit déterminer la correction à l'ordre suivant.
Pour déterminer
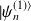 , on l'exprime dans la base
, on l'exprime dans la base
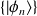 :
:
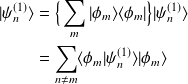
(Si
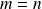 ,
,
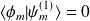 )
)
A partir de l'équation \ref{eq. :O1} (
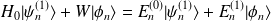 ), on obtient, en projetant sur
), on obtient, en projetant sur
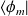 tel que (
tel que (
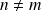 ):
):
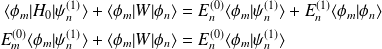
(où on a appliqué
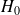 à gauche et utilisé le fait que
à gauche et utilisé le fait que
 ).
).
On déduit de ce résultat l'expression de la correction à l'état au premier ordre :
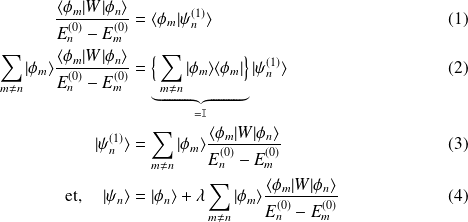
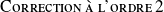
Partant de l'équation\ref{eq. :O2} :
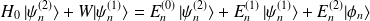
et en projetant sur
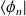 on obtient :
on obtient :
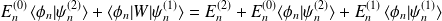
ce qui donne :
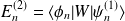
En remplaçant par l'expression de
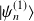 déjà calculée :
déjà calculée :
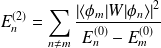
A l'ordre 2, l'énergie de l'état perturbé est :
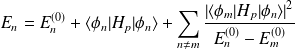
En général, un calcul à l'ordre deux est suffisant.
Pour le calcul de la correction à l'état,
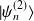 , on part, de la même manière que pour
, on part, de la même manière que pour
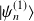 , de l'équation \ref{eq. :O2}, avec :
, de l'équation \ref{eq. :O2}, avec :
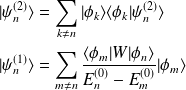
ce qui donne, après projection sur l'état
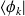 :
:
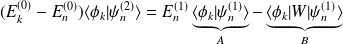
Le calcul des termes A et B donne :
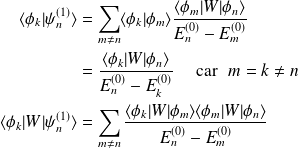
En utilisant la relation de fermeture on obtient :
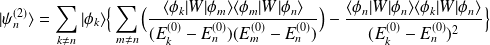
et finalement, on a pour l'état corrigé :
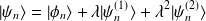
Remarque :
1- en raison des termes
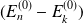 présents au dénominateur, on comprend pourquoi on s'est intéressé aux cas non dégénérés.
présents au dénominateur, on comprend pourquoi on s'est intéressé aux cas non dégénérés.
2- pour que le calcul perturbationnel soit justifié, on doit avoir :






