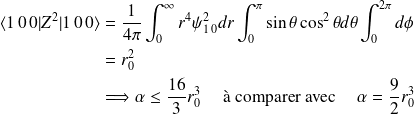Exemples d'Application
Exemple : Exemple 1
Soit une particule de masse
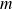 et de charge
et de charge
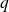 se déplaçant dans un potentiel harmonique à une dimension et soumise à un champ électrique faible
se déplaçant dans un potentiel harmonique à une dimension et soumise à un champ électrique faible
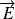 orienté dans la direction
orienté dans la direction
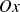 . On cherche à déterminer l'expression exacte de l'énergie puis à calculer la correction au premier ordre non nul de l'énergie et, en fin, à comparer ces deux quantités.
. On cherche à déterminer l'expression exacte de l'énergie puis à calculer la correction au premier ordre non nul de l'énergie et, en fin, à comparer ces deux quantités.
Soit
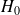 le hamiltonien de l'oscillateur chargé en absence du champ électrique :
le hamiltonien de l'oscillateur chargé en absence du champ électrique :
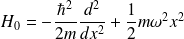
Son interaction avec le champ électrique se traduit par le terme :
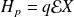 où
où
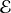 désigne l'amplitude du champ électrique (opérateur associé etc.)
désigne l'amplitude du champ électrique (opérateur associé etc.)
Le hamiltonien total s'écrit alors :
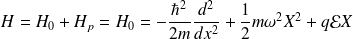
Une solution exacte peut être trouvée pour ce système sans recourir aux approximations. On pose :
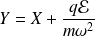 . On a :
. On a :
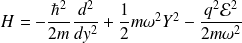
qui n'est autre que l'expression du hamiltonien d'un oscillateur à la quantité finie près
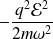 . Les énergies correspondantes sont :
. Les énergies correspondantes sont :
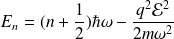
Pour un traitement par perturbations (
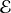 faible), on utilisera les opérateurs de création et d'annihilation. On rappelle quelques relations de la seconde quantification pour les opérateurs de création
faible), on utilisera les opérateurs de création et d'annihilation. On rappelle quelques relations de la seconde quantification pour les opérateurs de création
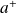 et d'annhililation
et d'annhililation
 :
:
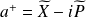 ,
,
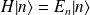 et
et
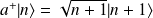
Au premier ordre, on a :
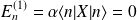
Et au deuxième ordre :
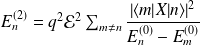
avec,
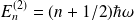 .
.
Le calcul des termes de la sommation donne
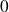 sauf pour deux termes consécutifs
sauf pour deux termes consécutifs
 et
et
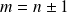 :
:
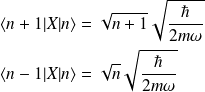
dans ces cas :
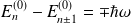 .
.
On obtient :
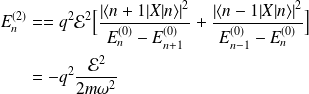
Ainsi,
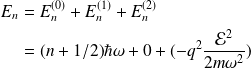
les niveaux d'énergie sont simplement décalés de la même quantité (
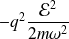 ).
).
La correction, à l'ordre
 , de l'état correspondant s'écrit :
, de l'état correspondant s'écrit :
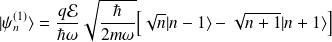
En fin, l'état est décrit par :
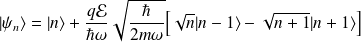
Exemple : Effet Stark
Un atome d'hydrogène est soumis à un champ électrique faible dirigé suivant
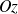 ,
,
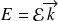 . L'atome est dans son état fondamental et on ignore le degré de liberté intrinsèque de spin. On se propose d'étudier l'effet de ce champ sur l'atome et de calculer une valeur approchée de la polarisabilité de l'atome.
. L'atome est dans son état fondamental et on ignore le degré de liberté intrinsèque de spin. On se propose d'étudier l'effet de ce champ sur l'atome et de calculer une valeur approchée de la polarisabilité de l'atome.
En absence du champ (
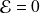 ), l'atome est décrit par le hamiltonien :
), l'atome est décrit par le hamiltonien :
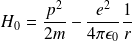
Les états propres sont les états
 , tels que :
, tels que :
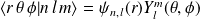
Si (
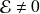 ), l'interaction est décrite par :
), l'interaction est décrite par :
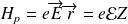 .
.
On a alors,
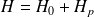 . Dans ce cas, l'atome d'hydrogène possède un état fondamental non dégénéré et des états excités dégénérés (
. Dans ce cas, l'atome d'hydrogène possède un état fondamental non dégénéré et des états excités dégénérés (
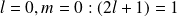 pour l'état fondamental et
pour l'état fondamental et
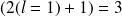 pour le premier état excité). Par conséquent, la théorie des perturbations s'applique uniquement à l'état fondamental
pour le premier état excité). Par conséquent, la théorie des perturbations s'applique uniquement à l'état fondamental
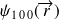 .
.
L'énergie de l'atome à l'ordre 2 s'écrit :
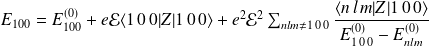
où
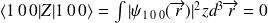
(en effet, les fonctions
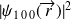 et
et
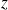 étant, respectivement, paire et impaire, l'intégrale est nulle).
étant, respectivement, paire et impaire, l'intégrale est nulle).
Il n'y a pas d'effet Stark linéaire (dépendant de
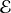 ) : l'atome dans son état fondamental n'a pas de moment dipôlaire électrique permanent. Il reste une contribution quadratique (terme en
) : l'atome dans son état fondamental n'a pas de moment dipôlaire électrique permanent. Il reste une contribution quadratique (terme en
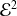 ), c'est l'effet Stark quadratique :
), c'est l'effet Stark quadratique :
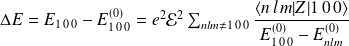
La polarisabilité de l'atome d'hydrogène est donnée par :
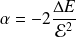
Soit
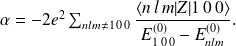
Pour calculer cette somme, on majore le terme en considérant le dénominateur comme constant (en notant
 le rayon de Bohr) :
le rayon de Bohr) :
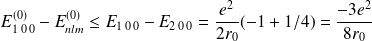
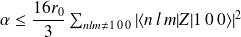
où :
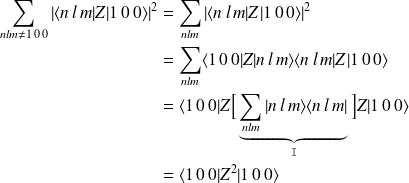
arrivés à ce stade du calcul, on peut remplacer par les expressions mathématiques,
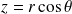 et
et
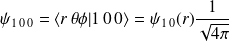 , soit :
, soit :