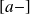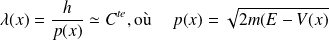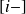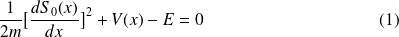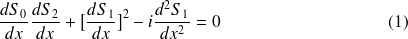Méthode de Wentzel-Kramers-Brillouin (WKB)
La mèthode
 est indiquée lorsque le terme d'énergie potentielle varie lentement en fonction de la position. Elle s'applique plus facilement aux cas unidimensionnels et à ceux pour lesquels l'équation de Schrödinger peut être ramenée à un cas unidimensionnel.
est indiquée lorsque le terme d'énergie potentielle varie lentement en fonction de la position. Elle s'applique plus facilement aux cas unidimensionnels et à ceux pour lesquels l'équation de Schrödinger peut être ramenée à un cas unidimensionnel.
Soit le hamiltonien à une dimension et indépendant du temps, défini par : $\qquad H = \frac{-\hbar^ 2}{2 m} \frac{d^ 2}{dx^ 2} + V(x)$
Si $V(x) = V_0 $ une constante, les solutions de l'équation $ H \psi(x) = E \psi(x)$ sont des combinaisons linéaires de fonctions telles que :
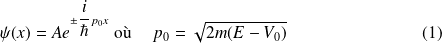
La condition d'avoir un potentiel variant lentement se traduit de deux manières équivalentes :
ou encore,
 Sur le schéma sont représentés (à titre illustratif), l'énergie
Sur le schéma sont représentés (à titre illustratif), l'énergie
 , le potentiel
, le potentiel
 et la longueur d'onde associée à la particule. Si
et la longueur d'onde associée à la particule. Si
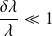 et si, sur l'échelle équivalente de longueur, le potentiel varie lentement, on peut alors utiliser l'approximation
et si, sur l'échelle équivalente de longueur, le potentiel varie lentement, on peut alors utiliser l'approximation
 .
.
Dans la limite classique,
 , on retrouve une situation où le potentiel varie très lentement.
, on retrouve une situation où le potentiel varie très lentement.
L'expression de
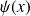 obtenue pour un potentiel variant très lentement suggère qu'on peut écrire de fa\c{c}on générale :
obtenue pour un potentiel variant très lentement suggère qu'on peut écrire de fa\c{c}on générale :

En substituant dans l'équation de Schr\"odinger on obtient :
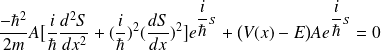
Soit,
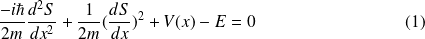
Jusqu'ici, aucune approximation n'est faite : cette équation est équivalente à l'équation de Schroedinger. Cependant, sa résolution est plus difficile et on doit alors faire des approximations.
Si
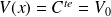 , alors
, alors
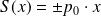 . Il s'ensuit que le terme
. Il s'ensuit que le terme
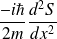 s'annule et comme il est proportionnel à
s'annule et comme il est proportionnel à
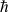 - et dans la limite classique
- et dans la limite classique
 , on peut, par conséquent, utiliser
, on peut, par conséquent, utiliser
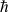 comme paramètre d'un développement limité.
comme paramètre d'un développement limité.

On substitue cette expression dans \ref{eq:S} et on identifie terme à terme les puissances égales en
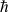 :
:
On peut résoudre ce système pour
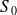 puis
puis
 ,
,
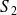 , etc..
, etc..
La méthode
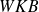 permet de trouver les deux premiers termes : \\
permet de trouver les deux premiers termes : \\
pour l'équation \ref{eq-i}, on suppose
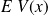 (il s'agit de la limite classique), on a :
(il s'agit de la limite classique), on a :
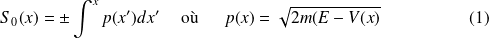
(
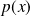 est la définition classique de l'impulsion.)
est la définition classique de l'impulsion.)
En utilisant cette expression dans l'équation \ref{eq-ii}, on obtient celle de
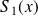 et en procèdant de même dans l'équation \ref{eq-iii}, on obtient celle de
et en procèdant de même dans l'équation \ref{eq-iii}, on obtient celle de
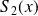 :
:
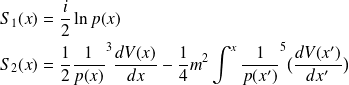
Remarque :
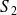 sera petit chaque fois que
sera petit chaque fois que
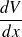 sera petit et que
sera petit et que
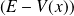 pas très proche de
pas très proche de
 .
.


Par conséquent, si
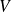 varie lentement et si
varie lentement et si
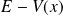 reste très différent de
reste très différent de
 , on peut se limiter à
, on peut se limiter à
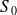 et
et
 .
.
Remarque : Si
 : la région est classiquement permise.
: la région est classiquement permise.
Si
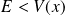 : la région est classiquement interdite.
: la région est classiquement interdite.
Si
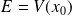 : le point
: le point
 de séparation est dit point de rebroussement.
de séparation est dit point de rebroussement.
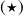

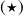 : En mécanique classique, ces points de rebroussement (ou de retour) peuvent être illustrés en considérant un potentiel unidimensionnel et indépendant du temps
: En mécanique classique, ces points de rebroussement (ou de retour) peuvent être illustrés en considérant un potentiel unidimensionnel et indépendant du temps
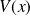 tel qu'une particule dont l'énergie totale, entre deux points
tel qu'une particule dont l'énergie totale, entre deux points
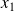 et
et
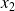 , est au plus égale au potentiel (
, est au plus égale au potentiel (
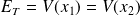 ), la particule ne peut pas s'échapper (
), la particule ne peut pas s'échapper (
 ) et rebrousse son chemin à chaque fois que
) et rebrousse son chemin à chaque fois que
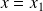 ou
ou
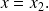

Dans le cas semi-classique, l'approximation
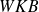 de la fonction d'onde s'écrit :
de la fonction d'onde s'écrit :

Si
 , on retrouve les expressions d'ondes planes :
, on retrouve les expressions d'ondes planes :

{\rem{Un critère de validité de la méthode
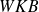 peut être obtenu en exigeant que le terme
peut être obtenu en exigeant que le terme
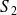 soit très petit :
soit très petit :
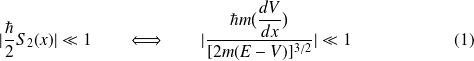
ce qui peut être satisfait si
 et si
et si
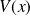 varie très lentement.
varie très lentement.
Dans le cas où
 ,
,
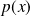 est imaginaire pure et la solution s'écrit :
est imaginaire pure et la solution s'écrit :
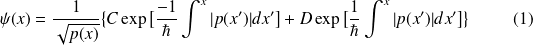
 sont des constantes arbitraires et la validité de la méthode
sont des constantes arbitraires et la validité de la méthode
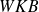 repose sur les mêmes conditions (\ref{condWKB}).
repose sur les mêmes conditions (\ref{condWKB}).

Les solutions obtenues (pour
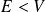 et
et
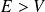 ) sont applicables lorsque
) sont applicables lorsque
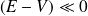 (ou
(ou
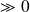 ) : elles sont des asymptotes à la solution totale.
) : elles sont des asymptotes à la solution totale.
Si on s'intéresse aux points de rebroussement (
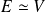 ), elles ne sont plus valables. Or, pour rendre compte de la continuité de la solution, on doit connecter (raccorder) les deux solutions de part et d'autre de chacun des points de rebroussement.
), elles ne sont plus valables. Or, pour rendre compte de la continuité de la solution, on doit connecter (raccorder) les deux solutions de part et d'autre de chacun des points de rebroussement.
soit un potentiel représenté par la courbe sur le schèma :
-------------------Courbe
Pour ce potentiel, on a :
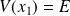 ,
,
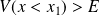 et
et
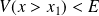 . L'espace est partagé en deux régions. Dans la région
. L'espace est partagé en deux régions. Dans la région
 ,
,
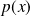 est réelle et la solution
est réelle et la solution
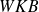 s'écrit :
s'écrit :
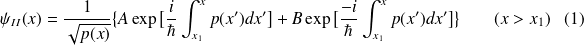
Dans la région
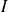 (classiquemet interdite)
(classiquemet interdite)
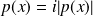 et la solution s'écrit :
et la solution s'écrit :
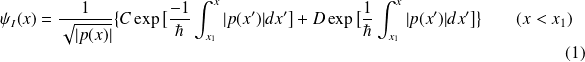
Remarque :
Par ce choix des bornes, les intégrales sont négatives. Les deux solutions sont des asymptotes pour
 très loin de
très loin de
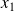 .
.

Lorsque
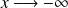 , on a nécessairement
, on a nécessairement
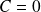 et après calcul, on obtient :
et après calcul, on obtient :

Si, de plus, on normalise la fonction d'onde, on obtient la formule de connexion suivante :
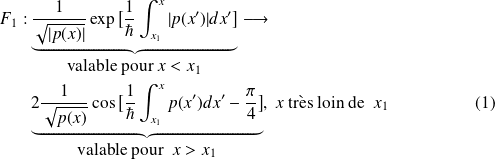
Malgré le fait que la fonction
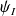 ne croît pas indéfiniment lorsque
ne croît pas indéfiniment lorsque
 , il est quand même utile de considérer le cas où elle croît exponentiellement en s'éloignant de
, il est quand même utile de considérer le cas où elle croît exponentiellement en s'éloignant de
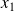 . La formule de connexion prend alors la forme suivante :
. La formule de connexion prend alors la forme suivante :
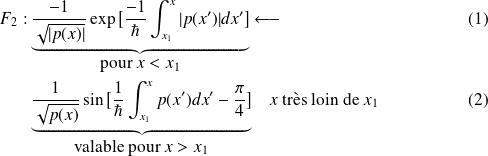
Il est à noter que les formules de connexions ne peuvent être utilisées que dans le sens des flêches :
 si on sait que la solution décroît pour
si on sait que la solution décroît pour
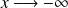 , on utilisera la première formule (cosinus)
, on utilisera la première formule (cosinus)
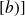 par contre, savoir que la fonction croît exponentiellement (pour
par contre, savoir que la fonction croît exponentiellement (pour
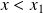 ) ne permet pas d'utiliser la deuxième formule (sinus)
) ne permet pas d'utiliser la deuxième formule (sinus)
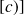 de fa\c{c}on similaire, si, pour
de fa\c{c}on similaire, si, pour
 , on sait que la solution est de type cosinus, on ne peut considérer que pour
, on sait que la solution est de type cosinus, on ne peut considérer que pour
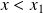 la solution décroît exponentiellement.
la solution décroît exponentiellement.
De manière conséquente : si la solution loin de
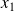 (
(
 ) est de la forme :
) est de la forme :
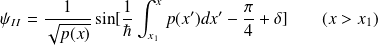
(où
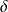 est une phase donnée), alors, la solution loin de
est une phase donnée), alors, la solution loin de
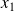 (i.e. pour
(i.e. pour
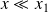 ) doit être une exponentielle croissante :
) doit être une exponentielle croissante :
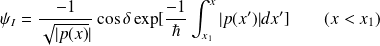
Dans le cas particulier où
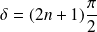 , avec
, avec
 , l'asymptote est une exponentielle décroissante.
, l'asymptote est une exponentielle décroissante.
%%---------------------------------------------- Fin Figure 3
Une étude identique donne les formules de connexion suivantes :
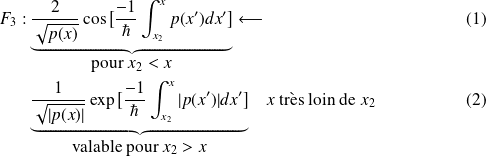
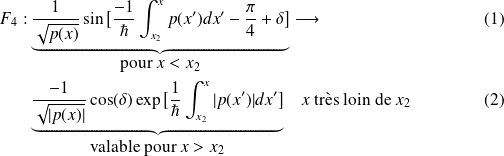
La dernière relation donne une exponentielle décroissante pour
 .
.
Exemple : Exemple 1 : calcul des niveaux d'énergie dans un puits de potentiel
On s'intéresse aux énergies des états liés dans un potentiel unidimensionnel
 .
.
%%--------------------------------------------Fin Courbe 4
On admet que pour chaque niveau d'énergie, il existe deux points
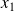 et
et
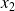 suffisamment séparés entre eux. On utilise en
suffisamment séparés entre eux. On utilise en
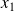 les formules de connexion pour la barrière gauche, et en
les formules de connexion pour la barrière gauche, et en
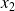 , celles pour la barrière droite. De plus, comme la fonction d'onde de l'état lié est de carré sommable, on doit avoir :
, celles pour la barrière droite. De plus, comme la fonction d'onde de l'état lié est de carré sommable, on doit avoir :
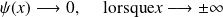
Le comportement de la solution pour
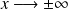 impose l'utilisation des formules de connexion :
impose l'utilisation des formules de connexion :
 en
en
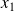 et
et
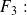 en
en
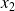 .
.
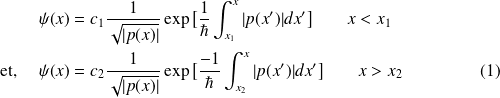
A l'intérieur du puits, la solution
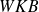 doit être un multiple soit du terme à droite de
doit être un multiple soit du terme à droite de
 soit du terme à gauche de
soit du terme à gauche de
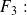 , ceci implique :
, ceci implique :
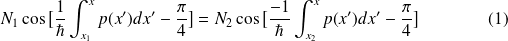
avec
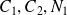 et
et
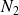 des constantes.
des constantes.
Cette égalité est vérifiée si :
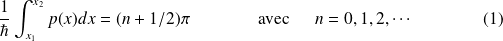
Cette équation n'est satisfaite que pour des valeurs discrètes de l'énergie :
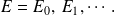 Ce sont les valeurs données par l'approximation
Ce sont les valeurs données par l'approximation
 pour les états liés.
pour les états liés.
Le nombre
 représente pour la solution à l'intérieur du puits le nombre de noeuds entre les deux points
représente pour la solution à l'intérieur du puits le nombre de noeuds entre les deux points
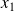 et
et
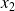 .
.
Remarque :
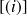 Il y a analogie avec la condition de quantification de Sommerfeld. En effet,
Il y a analogie avec la condition de quantification de Sommerfeld. En effet,

 et
et
 doivent être très (suffisamment) séparés
doivent être très (suffisamment) séparés
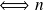 très grand.
très grand.

On applique la méthode
 au cas d'un oscillateur harmonique à 1-D, pour estimer la valeur des niveaux d'énergie :
au cas d'un oscillateur harmonique à 1-D, pour estimer la valeur des niveaux d'énergie :
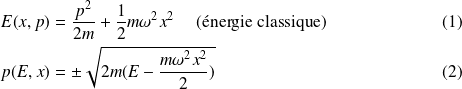
aux points de rebroussement
 et
et
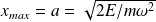 , on a
, on a
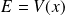 .
.
Pour obtenir l'expression de l'énergie quantifiée de l'oscillateur harmonique, on utilise la règle de quantification de Bohr-Sommerfeld :
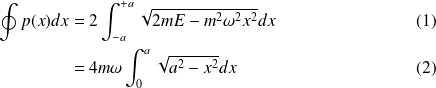
Si on pose
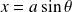 , on a :
, on a :
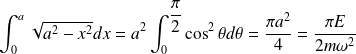
d'où, en remplaçant dans l'expression (\ref{B-S}) :
 . Puisque nous avons, d'un autre côté, pour deux variables conjugées
. Puisque nous avons, d'un autre côté, pour deux variables conjugées
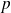 et
et
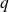 :
:
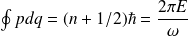 , on obtient, finalement,
, on obtient, finalement,

Ce qui est identique à l'énergie exacte de l'oscillateur harmonique.
Exemple : Exemple 2
Soit une particule sans spin et de masse
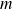 , se déplaçant dans une boîte unidimensionnelle tel que
, se déplaçant dans une boîte unidimensionnelle tel que
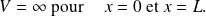
Dans ce cas, la règle de quantification s'écrit :
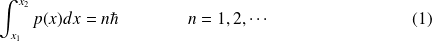
Le moment
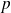 est constant dans le puits :
est constant dans le puits :
 . L'expression de l'énergie
. L'expression de l'énergie
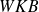 est alors :
est alors :

On retrouve le résultat pour une particule dans un puits infini.