Méthode Variationnelle
Principe
Il existe des situations où le hamiltonien d'un système est connu mais ne peut être résolu exactement ou par la méthode des perturbations introduite dans la section précédente. La méthode variationnelle permet d'obtenir une approximation des états propres liés et leurs valeurs propres associées.
Pour un hamiltonien indépendant du temps, on a :
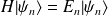. On suppose que
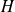admet au moins un état lié. Soit $|\phi \rangle un état correspondant à une fonction
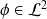et
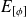la fonctionnelle définie par :
Remarque : On peut considérer comme fonctionnelle toute fonction qui prend pour argument une autre (ou plusieurs) fonction(s).
Il est clair que, si
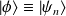, alors :
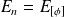. En effet :
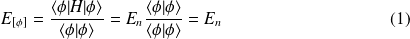
De plus, on montre que toute fonction
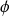, tel que
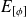est stationnaire, est une fonction propre de
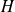, i.e.,
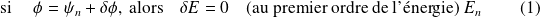
ou encore
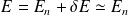
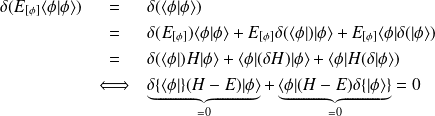
Sous forme intégrale, on a :
ce qui est équivalent à :
Ainsi, toute fonction
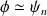, tel que
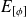est stationnaire, est solution de
.
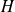Remarque :
l'équation de
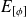est indépendante de
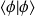et de la phase de
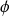,le résultat se retrouve dans le cas particulier
.
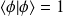L'équation de
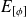donne une limite supérieure de l'énergie (
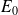) de l'état fondamental. On suppose, en effet, que l'on peut développer
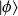dans la base propre de
:
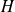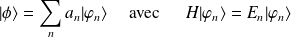
On soustrait
:
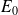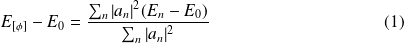
Comme
, (
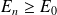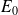étant l'énergie de l'état fondamental, donc la plus basse), on a :
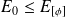
La méthode variationnelle (appelé aussi de Rayleigh-Ritz) consiste à calculer
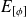à partir d'une fonction d'essai
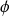qui dépend de certains paramètres. (
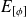dépend aussi de ces paramètres..)
On minimise
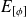pour obtenir la meilleure valeur approchée de
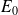qu'on peut avoir pour ce jeu de paramètres et de cette fonction
.
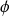Toute la question repose donc sur le choix de
!
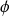On essaie de respecter les conditions initiales du problème étudié et de mettre à profit les propriétés de symétrie du système.
Exemple : Exemple 1
On étudie une particule, de masse
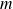, dans un puits carré infini et de largeur
.
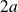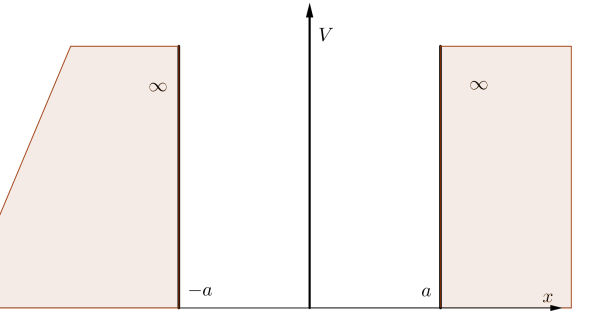
Dans ce cas, les solutions exactes sont connues :
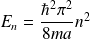, associées aux états
.
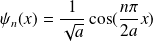L'état fondamental (
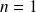) s'écrit :
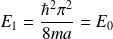et
.
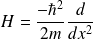On applique le principe variationnel de Rayleigh-Ritz : on suppose ne rien connaître de la solution exacte
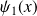et on cherche à estimer la valeur de
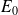. On exploite cependant quelques uns de ses comportements :
La fonction est paire et s'annule pour
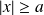, on choisit une fonction d'essai :
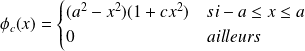
est le paramètre variationnel.
La première étape consiste à évaluer
:
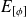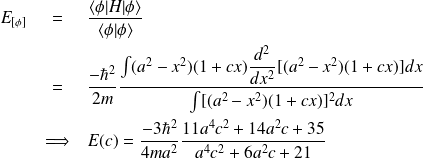
On minimise
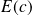par rapport à
:
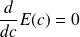
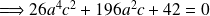
Il y a deux solutions à cette équation :
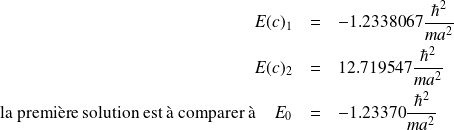
L'accord obtenu entre les deux valeurs est assez bon.
Exemple : Exemple 2
On se propose ici d'utiliser la méthode variationnelle pour calculer une valeur approchée de l'énergie de l'état fondamental de l'atome d'hydrogène.
On utilise le fait que la fonction ne s'annule qu'à l'infini (elle n'a pas de noeuds). De plus, l'état fondamental est de symétrie sphérique : il n'y a pas de dépendance en
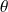et
.
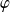On considère comme fonction d'essai (
étant un paramètre):
partant des expressions de
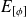et
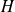(en posant
) :
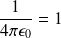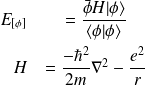
On a :
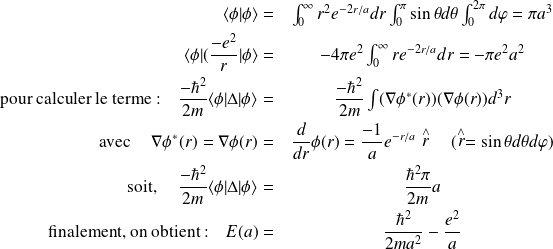
On minimise alors
:
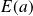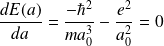
où
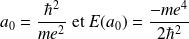
On retrouve le résultat exact : il est vrai que la fonction d'essai choisie,
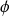, est comparable à la solution exacte.
