Cas Dégénérés
Cas dégénérés
Soit un système physique décrit par le hamiltonien non perturbé
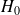dont le spectre est dégénéré et soumis à une perturbation
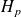tel que :
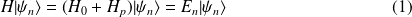
L'état d'énergie
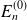est dégénéré
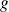fois, i.e. il existe
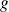états
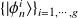tel que :
A l'ordre zéro de l'approximation, on peut développer l'état
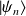sur les états
:
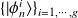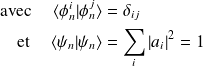
En substituant dans l'équation du hamiltonien, on écrit :
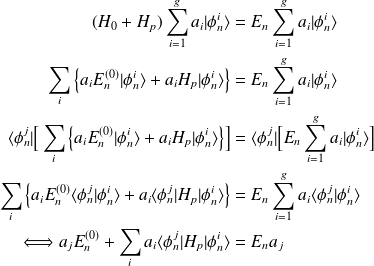
ce qu'on peut écrire sous la forme d'un système linéaire des coefficients
:
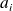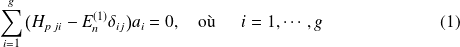
avec
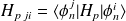et
.
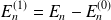Des solutions existent si $
:
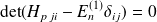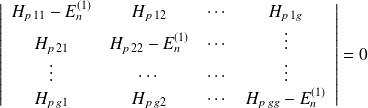
On obtient une équation de degré
en
qui, en général, admet
solutions (réelles) :
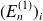. Ces racines sont des corrections au premier ordre des énergies
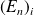de l'hamiltonien
.
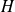Pour déterminer les coefficients
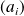on remplace dans l'équation séculaire (\ref{secu}) par ces racines. Le calcul des
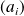permet d'écrire l'expression de
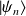à l'ordre zéro.
Les racines
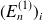sont en général différentes et, dans ce cas,
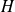admet un spectre non dégénéré.
L'état propre,
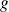-fois dégénéré de
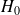associé à la valeur propre
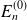est éclaté en
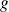sous-niveaux (états) d'énergies :
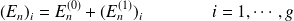
On dit alors que la perturbation lève totalement la dégénérescence. Cette levée de dégénérescence peut n'être que partielle, certaines racines restent égales.
Exemple : Exemple 1
On reprend l'exemple de l'effet Stark traité auparavant. On cherche à calculer l'énergie des états
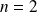lorsque l'atome d'hydrogène est placé dans un champ faible dirigé dans la direction
,
. On omet le moment de spin.
L'état
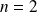correspond à l'énergie
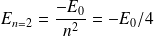, où
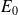désigne la constante de Rydberg (
).
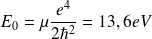Cet état est
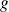-fois dégénéré :
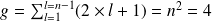. Les états correspondants sont indexés par les nombres quatiques
:
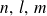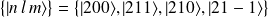
L'énergie d'interaction avec le champ est décrite par :
.
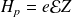On cherche les énergies propres associées, pour ce faire, on construit la matrice
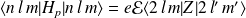, en utilisant les définitions :
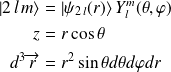
On peut également mettre à profit les règles de sélection et les propriétés de symétrie. En effet,
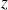ne dépend pas de
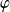, les éléments
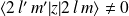si et seulement si
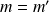. Ensuite,
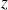étant impaire, les deux états
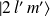et
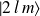doivent avoir des parités opposées. Il s'ensuit que les seuls termes non nuls sont ceux qui mettent en jeu les états
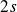et
(
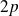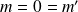), soit :
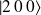et
.
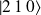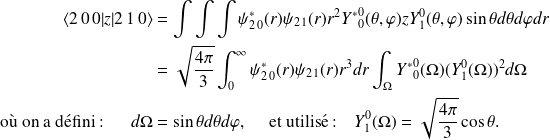
Le calcul donne :
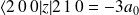, où
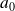est le rayon de Bohr.
Pour simplifier les écritures, on note les états comme suit :
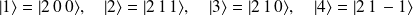
La matrice représentant
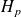s'écrit alors :
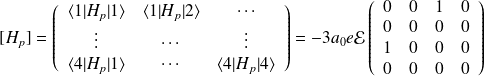
La diagonalisation de cette matrice donne les quatre valeurs propres :
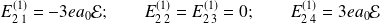
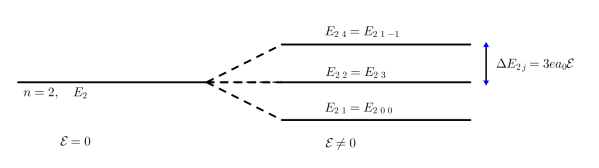
\textsc{Représentation des niveaux d'énergie}
Les états correspondants sont, par conséquent :
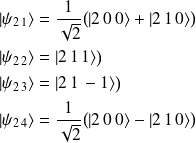
Sous l'action du champ
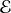, le niveau
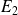se scinde en 4 niveaux dont deux sont encore dégénérés : elle n'est que partiellement levée,puisqu'en effet, les états
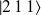et
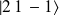restent associés à la même valeur propre
.
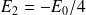