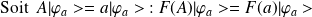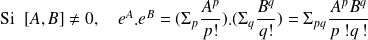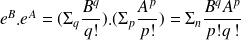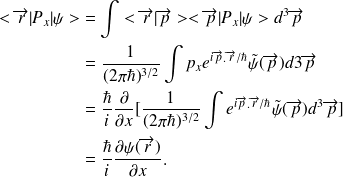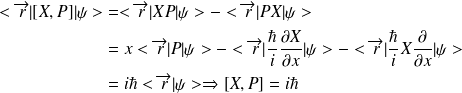Ensemble Complet d'Observables qui Commutent
Définition : a)- Théorème : Observables qui Commutent
*
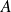et
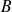observables tels que:
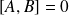
et
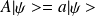alors
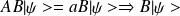est vecteur propre de
.
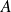* Si
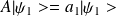et
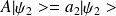alors
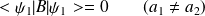
b)- ECOC :
Une suite d'observables
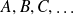forme un E.C.O.C. si ces observables commutent deux à deux et si chaque vecteur propre de leur base commune est défini de façon unique par la donnée des valeurs propres
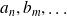des observables
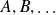respectivement .
c)- Exemples d'observables et de représentations :
Opérateur
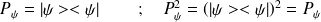
- P y hermitique :
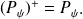
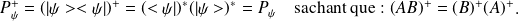
- valeurs propres de
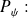
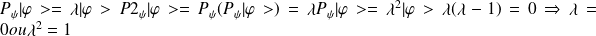
- vecteur propre :
.
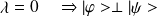
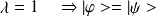- base : pour tout
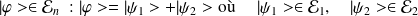
En effet,
Fonctions d'opérateurs :
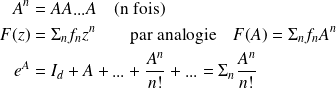
Si
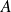est hermitien
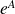l'est aussi.
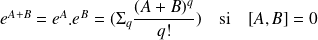
Trace d'un opérateur :
Rappels :
Représentations
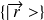et
:
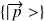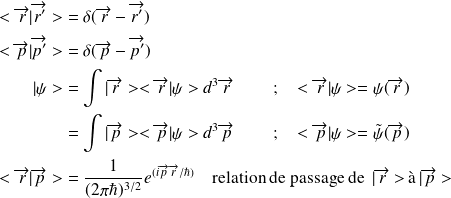
Calcul de
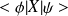
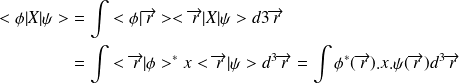
Conséquence :
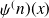désigne la dérivée
-ième de
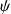par rapport à
.
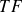désigne la Transformée de Fourrier.
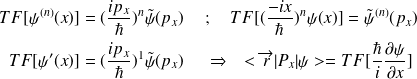
Le premier terme et le troisième s'annulant.
