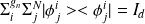Equations aux Valeurs Propres
Equations aux valeurs propres :
a) Equations aux valeurs propres :
Soit
l'opérateur associé à la variable dynamique
.
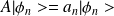
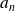est une valeur propre,
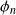un état propre du système correspondant à
.
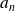Définition : Postulat 4 : Mesure
La mesure d'une grandeur physique ne peut donner comme résultat que l'une des valeurs propres de l'observable correspondante. L'ensemble des valeurs
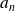est dit spectre de
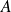, il peut être discret on continu.
Soit
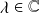, valeur propre de
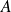associée à l'état propre (ou vecteur propre)
:
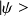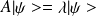
d'une manière générale on obtient les valeurs propres et vecteurs propres en résolvant l'équation :
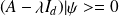
ou bien, en écriture matricielle :
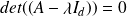(équation caractéristique)
Si à une valeur propre
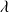sont associés
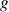vecteurs propres alors
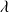est de dégénérescence
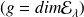où
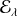désigne le sous-espace associé à
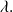
Soit
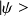normé et
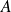un opérateur :
Définition : Théorèmes
* si
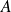est hermitien, ses valeurs propres sont réelles
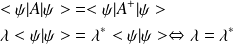
* Les vecteurs propres associés à des valeurs propres différentes d'un opérateur hermitien sont orthogonaux entre eux :
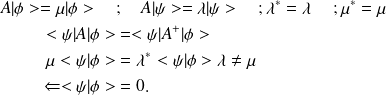
Définition : Postulat 5 :
Lorsqu'on mesure la grande physique
sur un système se trouvant dans l'état
normé, la probabilité d'obtenir comme résultat de mesure la valeur propre
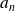de l'observable
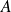associée à
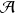est :
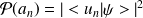cas discret
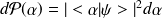cas continu
Cas Général
Cas dégénérés :
Soit
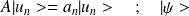un état propre.
Si la valeur propre est
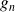fois dégénérée, les vecteurs de la base sont indexés comme suit:
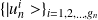
on écrit :
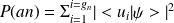
Soit le projecteur sur
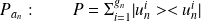
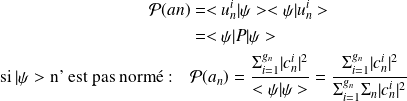
Définition : Postulat 6 : Valeur Moyenne
Si une série de mesures d'une variable dynamique
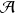est effectuée sur un ensemble de systèmes, décrit par
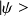, la valeur moyenne de cette variable dynamique (associée à l'observable
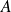), est :
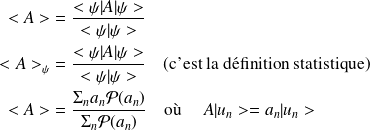
Si
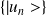est une base, et les valeurs propres sont simples,
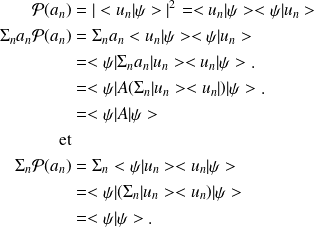
Remarque : Théorèmes
Si
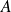et
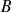commutent et si
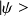est ket propre associé à
, alors
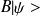est ket propre de
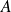associé à la même valeur propre
.
Si
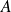et
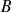commutent et si
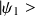et
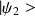sont deux kets propres de
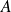associés à deux valeurs propres distinctes alors
.
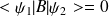Si
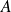et
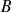commutent, on peut construire une base de l'espace des états constituée par les kets propres communs à
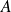et à
.
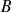Preuve :
1- Soit
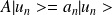et
.
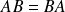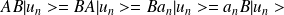
2-
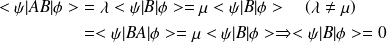
3-
Remarque :
S'il existe une base formée de kets propres de
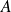et de
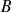, alors
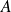et
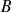commutent.
Ces relations sont vraies aussi pour les observables.
Définition : Théorème
b) Observables :
Théorème : Une observable est un opérateur hermitien tel que l'on peut former avec ses vecteurs propres une base de l'espace des états
.
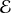Remarque : Si
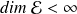cela est vrai
Si
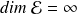cela n'est pas toujours vrai.
Soit
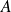hermitien ayant des valeurs propres
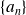avec
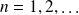et des états propres
.
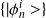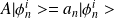
si
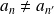on a
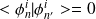
et
.
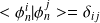Par définition : si
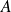hermitien, c'est une observable si
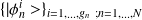forme une base, or on a la relation de fermeture :
