Evolution dans le Temps
Opérateur Evolution
Jusqu'ici, nous avons considéré les systèmes physiques dans des états stationnaires ou ne dépendant pas du temps. L'étude de l'évolution dans le temps d'un système quantique est représentée par un opérateur agissant sur l'état du système.
Définition : Postulat 7 : Evolution dans Le Temps
L'évolution dans le temps de l'état décrivant un système est déterminée par l'équation de Schrödinger dépendant du temps :
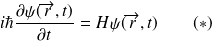
où
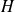est le hamiltonien ou l'opérateur associé à l'énergie totale du système.
est une équation différentielle du premier ordre en
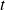: connaissant
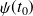, il est possible de déterminer
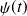pour
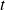quelconque .
Remarque : comme on s'intéresse au temps, on omettra lorsqu'il n'y a pas de confusion, la variable d'espace
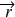
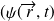sera noté simplement
).
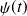On introduit l'opérateur évolution
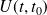tel que :
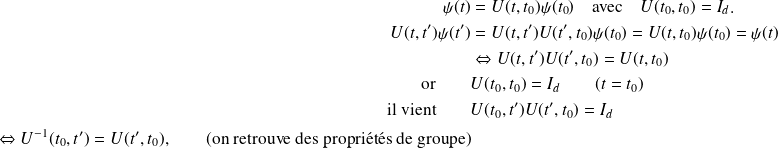
de plus on peut montrer que
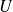satisfait la relation :
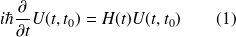
La conservation de la probabilité nécessite :
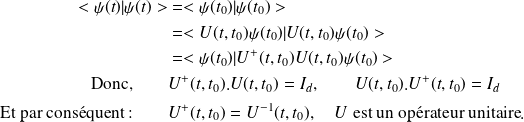
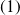a une solution qui satisfait à l'équation
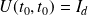et qui s'écrit :
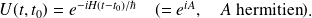
Dans le cas où le système est conservatif :
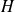est indépendant du temps.
Une solution formelle de l'équation de Schrödinger dépendant du temps est donnée par :
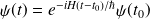
Exemple : Exemple d'une particule dans un potentiel V(r) ne dépendant pas de t
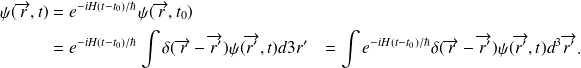
En écrivant la relation de fermeture dans la base des fonctions propres
:
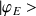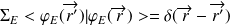
et en utlisant:
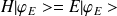il vient,
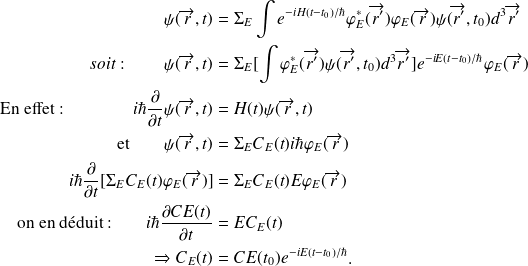
On retrouve la principe de superposition et le fait que dans le cas d'un potentiel indépendant du temps, les états stationnaires
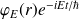
sont des solutions particulières de l'équation de Schrödinger dépendant du temps .
a)- Variation de la valeur moyenne :
Soit
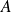une observable.
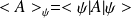la valeur moyenne de
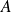dans l'état
normé.
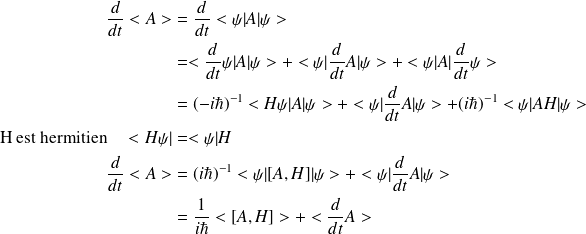
Si
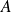ne dépend pas de
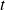et si
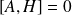, l'observable
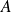est une constante du mouvement .
Exemple :
-1- Pour
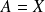, et pour un système décrit par le hamiltonien
,
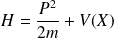on a
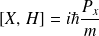et
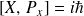, ce qui donne :
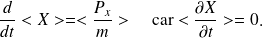
-2-
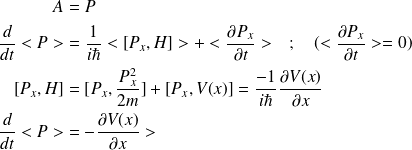
b)- Analogie avec la Mécanique Classique :
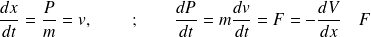dérive d'un potentiel.
