Etat d'un Système
Définitions
En Physique classique, l'état dynamique d'un système est déterminé à chaque instant par la connaissance de quantités physiques – les variables dynamiques – telles que la position et la quantité de mouvement des particules qui constituent le système. Ces variables peuvent, en principe, être mesurées simultanément avec une précision infinie.
En mécanique quantique, la situation est différente en raison de l'importance de l'acte de « mesurer » et l'état d'un système ne peut être prédit. En effet, quand on mesure une variable, l'état dynamique du système évolue et change de manière imprédictible, et selon le principe de Heisenberg, sa détermination est limitée par l'incertitude avec laquelle deux variables conjuguées peuvent être mesurées simultanément. Comment décrire alors, mathématiquement, l'état d'un système à un instant
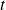 donné ? Et comment déterminer l'état de ce système à l'instant
donné ? Et comment déterminer l'état de ce système à l'instant
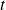 quelconque si l'on connaît son état à un instant
quelconque si l'on connaît son état à un instant
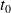 ?
?
D'un autre côté, la mécanique quantique permet de prédire le nombre n de fois où on peut trouver une certaine valeur de la mesure après une mesure sur un ensemble
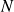 de particules identiques et indiscernables. Le rapport
de particules identiques et indiscernables. Le rapport
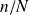 définit alors la probabilité de trouver le système dans l'état ayant pour valeur propre cette mesure. Comment, étant donné l'état du système, exprimer cette probabilité et prévoir les résultats de mesure des diverses grandeurs étudiées ?
définit alors la probabilité de trouver le système dans l'état ayant pour valeur propre cette mesure. Comment, étant donné l'état du système, exprimer cette probabilité et prévoir les résultats de mesure des diverses grandeurs étudiées ?
Afin d'étudier ces aspects de la mécanique quantique on fait appel à des postulats qui seront énoncés et formulés ci-après.
Définition : Postulat 1
A un ensemble de systèmes physiques on peut, dans certains cas, associer une fonction d'onde, ou fonction d'état, qui contient toutes les informations concernant ce système. Cette fonction est en général complexe et peut être multipliée par un nombre complexe sans en modifier la signification physique.
Remarques :
- « dans certains cas » fait allusion aux ensembles statistiques de particules qui doivent être étudiés dans le cadre de la physique statistique.
- en principe, et d'après la définition de la fonction d'onde, on considère des ensembles bien que par abus de langage on associe la fonction d'onde à un système particulier (au lieu d'un ensembles de systèmes identiques) : on parle ainsi de fonction d'onde associée à un électron alors qu'en fait il s'agit d'une fonction d'onde associée à un ensemble d'électrons identiques indiscernables tel que la fonction décrive la probabilité de trouver un de ces électrons dans un état donné. La fonction étant de carré sommable, en sommant sur tout l'espace on normalise à l'unité.
En traduisant le premier postulat, deux fonctions telles que
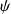 et
et
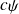 , où
, où
 est une constante complexe arbitraire, représentent le même état , on choisit alors la constante c de sorte que l'on ait :
est une constante complexe arbitraire, représentent le même état , on choisit alors la constante c de sorte que l'on ait :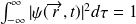
On remarque que si on écrit cette constante sous la forme
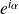 : où
: où
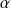 est un nombre réel, alors les deux fonctions
est un nombre réel, alors les deux fonctions
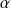 et
et
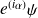 décrivent le même état tout en conservant la norme de la fonction d'onde et la densité de probabilité reste inchangée :
décrivent le même état tout en conservant la norme de la fonction d'onde et la densité de probabilité reste inchangée :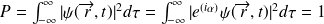
Généralisation :
On considère un ensemble de
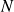 systèmes identiques (et sans degrés de liberté internes), la fonction d'état (
systèmes identiques (et sans degrés de liberté internes), la fonction d'état (
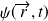 ou
ou
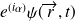 ) associée à cet ensemble dépend, dans l'espace de configuration, des coordonnées
) associée à cet ensemble dépend, dans l'espace de configuration, des coordonnées
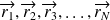 et du temps
et du temps
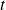 :
:
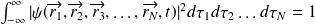
De même :
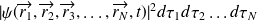
définit la probabilité de trouver, à l'instant
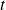 , le système (la particule)
, le système (la particule)
 dans le volume
dans le volume
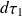 autour de
autour de
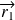 et le système
et le système
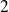 dans le volume
dans le volume
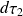 autour de
autour de
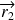 et ainsi de suite..
et ainsi de suite..
On écrit aussi la probabilité de trouver, à l'instant t, la particule
 dans le volume
dans le volume
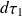 autour de
autour de
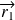 indépendamment des positions des autres particules :
indépendamment des positions des autres particules :
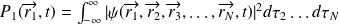
Définition : Postulat 2 : Principe de superposition
Les états dynamiques d'un système sont linéairement superposables.
Remarques:
i) - étant donné
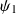 et
et
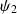 deux fonctions d'onde décrivant deux états possibles d'un ensemble de systèmes quantiques, alors toute combinaison linéaire
deux fonctions d'onde décrivant deux états possibles d'un ensemble de systèmes quantiques, alors toute combinaison linéaire
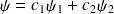 , où
, où
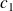 et
et
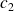 sont des nombres complexes, est aussi associée à un état possible de cet ensemble.
sont des nombres complexes, est aussi associée à un état possible de cet ensemble.
ii) - La phase relative entre les deux fonctions d'onde joue un rôle important dans le calcul de
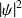 .
.
Fonctions d'onde dans l'espace des moments :
Pour décrire l'état de la particule aussi utiliser la fonction d'état
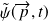 associée à cet ensemble, exprimée dans l'espace de configuration des moments, en fonction de
associée à cet ensemble, exprimée dans l'espace de configuration des moments, en fonction de
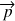 et du temps
et du temps
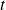 . C'est la transformée de Fourier de
. C'est la transformée de Fourier de
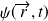 et elle vérifie donc :
et elle vérifie donc :