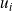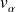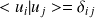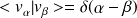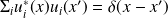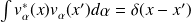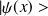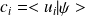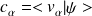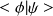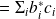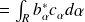Notation de Dirac
Etat d'un Système
Tout état quantique d'une particule sera caractérisé par un vecteur d'état, représenté par
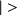, appartenant à un espace abstrait
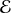(appelé espace des états).
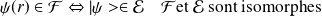
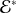désigne le dual de
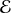et ses éléments sont notés
.
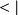Le produit scalaire s'écrit :
.
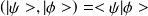Propriétés :
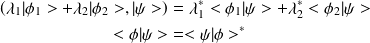
Conjugaison Hermitien
Si à
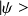on fait correspondre
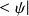, on dit que le bra est le conjugué hermitique du ket et inversement .
Définition : Postulat 3 : Variable Dynamique
A chaque variable dynamique on associe un opérateur linéaire. Cet opérateur est une observable.
Opérateurs
i)- Opérateur linéaire :
A opérateur tel que si
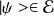, alors il existe
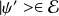, tel que:
.
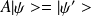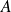est linéaire si :
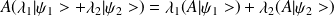
Produit de deux opérateurs :
,
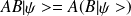En général
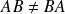. On définit :
.
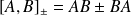Remarque : par la suite on omettra le signe (
) dans l'expression du commutateur
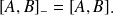
Exemples :
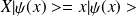
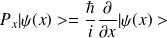
ii) Opérateur adjoint-Opérateur hermitique :
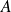et
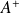sont adjoints si
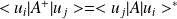
ou bien
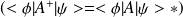
Si de plus
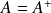alors
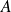et
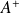sont hermitiens.
Exemples :
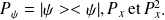
Propriétés :
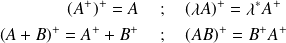
Le produit de deux opérateurs hermitiens
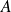et
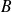n'est hermitien que si
.
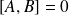Représentations dans l'Espace des Etats
i) Bases
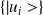et
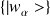
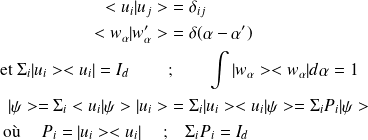
ii) kets et bras :
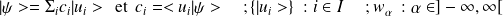
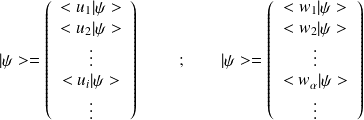
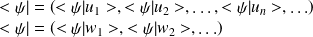
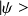et
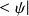sont deux matrices conjuguées hermitiennes.
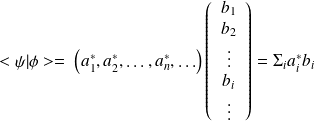
D'où on déduit l'expression de la norme :
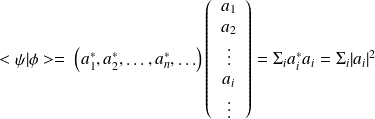
iii) Opérateurs : Soit
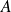un opérateur.
On écrit :
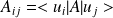et
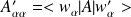
respectivement, les éléments de la matrice A dans
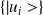et
.
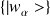Soit
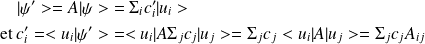
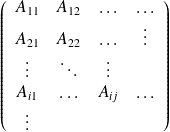
Si
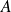est hermitien,
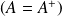alors
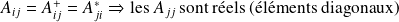
Rappel : Résumé
Base discrete (
| Base continue (
| |
Orthonormation : |
|
|
R. fermeture : |
|
|
Composition :
|
|
|
Produit scalaire :
|
|
|
